2019 ICPC Universidad Nacional de Colombia Programming Contest
A - Amazon
不会做 T_T
B - Boring Non-Palindrome
签到题 暴力
- 给定字符串,问至少在末尾添加多少个字符使得字符串变成回文串
因为数据范围很小可以O(n2),所以直接枚举末尾添加0至|s|个字符判断是否为回文串即可
/*
* @Author: Roark
* @School: BIT
*/
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long LL;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 10000 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int gcd(int a, int b)
{
return b?gcd(b,a%b):a;
}
char s[MAXN];
char ans[MAXN];
char temp[MAXN];
int num=INF;
void solve()
{
//Chtholly_is_so_cute
scanf("%s",s);
int len=strlen(s);
for(int i=0;i<len;i++)
{
memset(temp,0,sizeof(temp));
bool flag=1;
for(int j=0;j<=i;j++)
{
temp[j]=s[j];
}
for(int j=1;j<=i;j++)
{
temp[i+j]=temp[i-j];
}
for(int j=0;j<len;j++)
{
if(temp[j]!=s[j])
{
flag=0;
break;
}
}
if(flag)
{
if(num>2*i+1)
{
num=2*i+1;
strcpy(ans,temp);
}
}
}
for(int i=0;i<len;i++)
{
memset(temp,0,sizeof(temp));
bool flag=1;
for(int j=0;j<=i;j++)
{
temp[j]=s[j];
}
for(int j=1;j<=i+1;j++)
{
temp[i+j]=temp[i-j+1];
}
for(int j=0;j<len;j++)
{
if(temp[j]!=s[j])
{
flag=0;
break;
}
}
if(flag)
{
if(num>2*i+2)
{
num=2*i+2;
strcpy(ans,temp);
}
}
}
printf("%s\n",ans);
}
int main()
{
solve();
return 0;
}
C - Common Subsequence
DP (最长公共子序列)
- 给定两个基因序列,由'A'、'T'、'G'、'C'组成的字符串
- 问是否有血缘关系,若存在长度大于0.99×len的公共子序列,则有血缘关系
最长公共子序列的变形,先说说最长公共子序列的dp转移
$$ dp[i,j] = dp[i-1,j-1]+1 \qquad if \quad x_i = y_j $$
$$ dp[i,j] = max(dp[i,j-1],dp[i-1,j]) \qquad if \quad x_i \neq y_j $$
因为这里要求公共子序列长度大于0.99len,所以只需要在0.01len的范围内dp就可以了
/*
* @Author: Roark
* @School: BIT
*/
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long LL;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int gcd(int a, int b)
{
return b?gcd(b,a%b):a;
}
char aa[MAXN],bb[MAXN];
int dp[2][MAXN];
void solve()
{
//Chtholly_is_so_cute
scanf("%s%s",aa+1,bb+1);
int len=strlen(aa+1);
int fault=len/100;
int v=1;
for(int i=1;i<=len;i++)
{
for(int j=max(1,i-fault);j<=i+fault&&j<=len;j++)
{
if(aa[i]==bb[j])
{
dp[v][j]=dp[v^1][j-1]+1;
}
else
{
dp[v][j]=max(dp[v^1][j],dp[v][j-1]);
}
}
v^=1;
}
if(dp[v^1][len]>=len-fault)
{
printf("Long lost brothers D:\n");
}
else
{
printf("Not brothers :(\n");
}
}
int main()
{
solve();
return 0;
}
D - Do Not Try This Problem
分类 + 并查集?
- 给定字符串s,问所有操作后的字符串是什么
- 只有一种操作,将 i+bk(b=0,1,...,a) 位置的字符替换为字符c
离线操作,可以分为两种情况。
1)替换次数较少的时候,即a较小时,我们可以暴力更新。
2)替换次数较多的时候,我们可以枚举所有的k,从后往前的更新字符串,对于相同的k,后更新的会覆盖先更新的点,所以当遇到已更新过的点时,无需再次更新,可以直接跳转到已更新的区间末尾,如果在当前需要更新的范围内则继续更新。这里我们就可以使用并查集进行维护。
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f;
const int MAXN = 100000+10;
char s[MAXN], c[MAXN];
int ans[MAXN];
int fa[MAXN];
int find( int x ){
if( fa[x] == x ) return x;
else return (fa[x] = find(fa[x]));
}
int n, q;
struct Query{
int i, a, k, id;
Query(){}
Query( int i, int a, int k, int id ) : i(i), a(a), k(k), id(id) {}
};
vector<Query>v;
bool cmp( Query x, Query y ){
if( x.a == y.a ) return x.id > y.id;
return x.a < y.a;
}
void solve()
{
int ii, aa, kk;
for( int qq = 1; qq <= q; qq++ ){
getchar();
scanf("%d %d %d %c", &ii, &aa, &kk, &c[qq]);
if( aa > 100 ){
for(int i = ii; i <= ii+aa*kk; i += aa ){
ans[i] = qq;
}
continue;
}
v.push_back( Query( ii, aa, kk, qq) );
}
sort( v.begin(), v.end(), cmp );
int len = v.size();
for(int ii = 0; ii < len; ii++ ){
if( ii == 0 || v[ii].a != v[ii-1].a ){
for(int j = 0; j <= n+1; j++ ) fa[j] = j;
}
for( int j = find(v[ii].i); j <= v[ii].i+v[ii].a*v[ii].k; j = find(j) ){
ans[j] = max( ans[j], v[ii].id );
fa[j] = j+v[ii].a < n+1 ? j+v[ii].a : n+1;
}
}
for(int i = 1; i <= n; i++ ){
if( ans[i] ) s[i] = c[ans[i]];
}
printf("%s\n", s+1);
}
int main(int argc, char * argv[])
{
scanf("%s", s+1);
n = strlen( s+1 );
scanf("%d", &q);
solve();
return 0;
}
E - Extreme Image
扫描线 + 线段树
- 二维平面上分布很多散点
- 问用以原点为中心的环形(两个同心圆的非重合部分),固定宽度为 d(即同心圆半径差为d)
- 再在环形基础上取角度为 a 的扇形,即两个扇形的非重合部分,如图所示
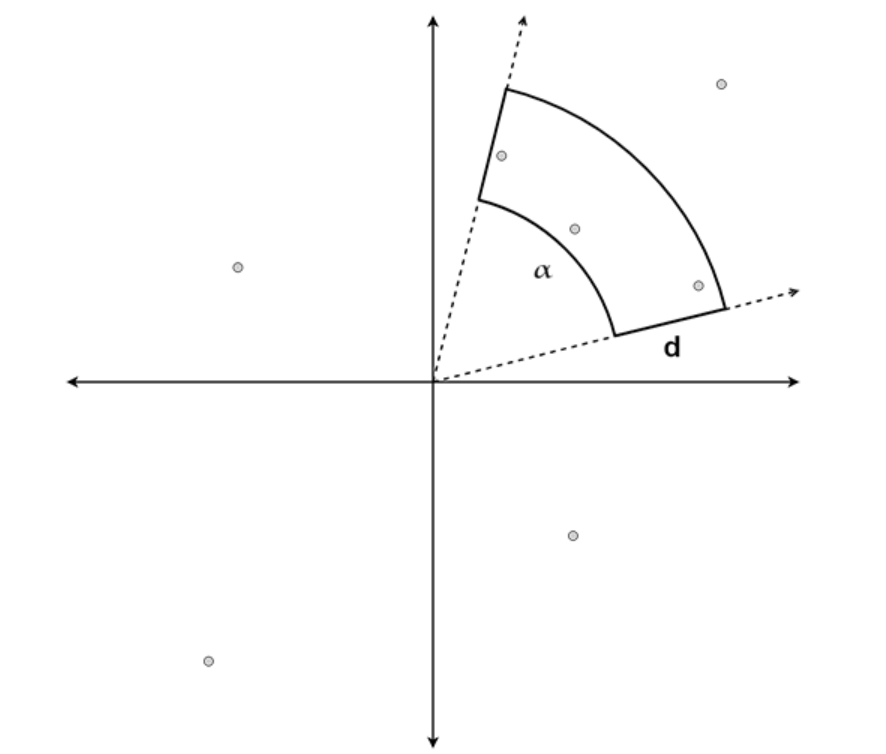
- 问该图形最多覆盖多少个散点
扫描线处理内圆半径r,由于r范围是1e5,所以可以暴力枚举所有的r。(范围更大则需要离散化)
每次移动扫描线的时候把r-1的删除,把r+d的加入线段树。
线段树用角度划分,底层节点表示角度在[w-a,w]的范围内,所以对于任意w0的删增,即修改区间[w0,w0+a],维护最大值即可。
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
#define ls (rt<<1)
#define rs (rt<<1|1)
const int INF = 0x3f3f3f3f;
int n, d, a1, a2, w1, w2, r;
struct node{
int w1, w2, op;
node(){}
node( int w1, int w2, int op ) : w1(w1), w2(w2), op(op) {}
};
vector<node>e[200000+10];
struct Tree{
int l, r;
int res, lz;
}t[36000*8+10];
void build( int l, int r, int rt ){
t[rt].l = l; t[rt].r = r;
if( l == r ) return;
int mid = (l+r)>>1;
build( l, mid, ls );
build( mid+1, r, rs );
}
void push_down( int rt ){
t[ls].res += t[rt].lz;
t[rs].res += t[rt].lz;
if( t[ls].l != t[ls].r ) t[ls].lz += t[rt].lz;
if( t[rs].l != t[rs].r ) t[rs].lz += t[rt].lz;
}
void push_up( int rt ){
t[rt].res = max( t[ls].res, t[rs].res );
}
void update( int l, int r, int op, int rt ){
if( l <= t[rt].l && r >= t[rt].r ){
t[rt].res += op;
t[rt].lz += op;
return;
}
if( t[rt].lz ){
push_down( rt );
t[rt].lz = 0;
}
int mid = (t[rt].l+t[rt].r)>>1;
if( mid >= r ) update( l, r, op, ls );
else if( mid < l ) update( l, r, op, rs );
else{
update( l, r, op, ls );
update( l, r, op, rs );
}
push_up( rt );
}
void solve()
{
build( 1, 36000, 1 );
int ans = 0;
for(int i = 0; i <= 100000; i++ ){
for(int j = 0; j < e[i].size(); j++ ){
update( e[i][j].w1, e[i][j].w2, e[i][j].op, 1 );
}
ans = max( ans, t[1].res );
}
printf("%d\n", ans);
}
int main(int argc, char * argv[])
{
scanf("%d %d %d.%d", &n, &d, &a1, &a2);
a1 = a1*100+a2;
for(int i = 1; i <= n; i++ ){
scanf("%d %d.%d", &r, &w1, &w2);
w1 = w1*100+w2;
if( w1+a1+1 > 36000 ){
e[r].push_back( node( w1+1, 36000, 1 ) );
e[r].push_back( node( 1, w1+a1+1-36000, 1 ) );
e[r+d+1].push_back( node( w1+1, 36000, -1 ) );
e[r+d+1].push_back( node( 1, w1+a1+1-36000, -1 ) );
}else{
e[r].push_back( node( w1+1, w1+a1+1, 1 ) );
e[r+d+1].push_back( node( w1+1, w1+a1+1, -1 ) );
}
}
solve();
return 0;
}
F - Fraction Formula
模拟
- 给出一个分数加减法的中缀表达式,有括号,计算答案
先预处理括号,全部变成正负数的加法运算
因为分母限制最大为20,所以分别计算分母相同的分数和,最后再通分、加和、约分即可
/*
* @Author: Roark
* @School: BIT
*/
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long LL;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 2e5 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
LL gcd(LL a, LL b)
{
return b?gcd(b,a%b):a;
}
int sta[MAXN];
int ttop;
char str[MAXN];
LL cnt[30];
char temp[20];
LL all;
void add(char *s, int op)
{
int len=strlen(s);
if(len==0)
{
return ;
}
int i=0;
int a=0,b=0;
for(i=0;s[i]!='/';i++)
{
a=a*10+s[i]-'0';
}
for(i=i+1;i<len;i++)
{
b=b*10+s[i]-'0';
}
if(op==1)//+
{
cnt[b]+=a;
}
else
{
cnt[b]-=a;
}
}
void solve()
{
//Chtholly_is_so_cute
int len=strlen(str);
memset(cnt,0,sizeof(cnt));
ttop=0;
for(int i=0;i<len;i++)
{
if(str[i]=='('&&str[i-1]=='-')
{
str[i]='$';
sta[++ttop]=-1;
}
else if(str[i]=='(')
{
sta[++ttop]=1;
}
else if(str[i]==')')
{
int d=sta[ttop--];
if(d==-1)
{
str[i]='$';
}
}
}
int v=0;
for(int i=0;i<len;i++)
{
if(str[i]=='+'&&v==1)
{
str[i]='-';
}
else if(str[i]=='-'&&v==1)
{
str[i]='+';
}
else if(str[i]=='$')
{
v^=1;
}
else if(str[i]==')'||str[i]=='(')
{
str[i]='#';
}
}
int p=0;
int top=0;
int op=1;
while(1)
{
if(p==len)
{
break;
}
else if(str[p]=='+')
{
temp[top++]='\0';
add(temp,op);
op=1;
top=0;
p++;
}
else if(str[p]=='-')
{
temp[top++]='\0';
add(temp,op);
op=0;
top=0;
p++;
}
else if(str[p]=='#'||str[p]=='$')
{
p++;
continue;
}
else
{
temp[top++]=str[p++];
}
}
temp[top++]='\0';
add(temp,op);
LL a=0,b=all;
for(int i=1;i<=20;i++)
{
a+=cnt[i]*all/i;
}
if(a==0)
{
printf("0/1\n");
return;
}
LL g=gcd(abs(a),abs(b));
printf("%lld/%lld\n",a/g,b/g);
}
int main()
{
all=1LL*2*2*2*2*3*3*5*7*11*13*17*19;
while(~scanf("%s",str)) solve();
return 0;
}
/*
(8/3+4/5-(9/3-5/1+3/2))+2/1
*/G - Graduation
贪心
- 一共n门课程,有些课程有一门先修课,即必须修完先修课才能修本门课程
- Potato每学期只能最多修k门课,问他最少需要几学期才能修完所有的课
可以按照先修课关系建图,形成森林结构
贪心策略:先修高度更高的节点(贪心证明略)
P.s. 贪心题就是把所有能想到的贪心策略全部写上去,最后答案谁更优取谁。→_→
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
#define pii pair<int,int>
#define fi first
#define se second
const int INF = 0x3f3f3f3f;
const int MAXN = 10000+10;
int n, k;
int a[MAXN];
int b[MAXN];
int tmp[20];
vector<int>e[MAXN];
struct cmp{
bool operator()( pii a, pii b ){
return a.se < b.se;
}
};
void dfs( int x ){
if( e[x].size() == 0 ){
return;
}
for( int i = 0; i < e[x].size(); i++ ){
int to = e[x][i];
dfs( to );
b[x] = max( b[x], b[to]+1 );
}
}
void solve()
{
priority_queue< pii, vector<pii>, cmp>q;
for(int i = 1; i <= n; i++ ){
if( a[i] == 0 ){
dfs( i );
q.push( mp( i, b[i] ));
}
}
int cnt = 0;
int ans = 0;
while( cnt < n ){
int cntt = k;
for(int j = 1; j <= k; j++ ){
if( q.empty() ){
cntt = j-1;
break;
}
tmp[j] = q.top().fi;
q.pop();
}
cnt += cntt;
for(int j = 1; j <= cntt; j++ ){
for(int p = 0; p < e[tmp[j]].size(); p++ ){
int to = e[tmp[j]][p];
q.push( mp( to, b[to] ));
}
}
ans++;
}
printf("%d\n", ans);
}
int main(int argc, char * argv[])
{
scanf("%d %d", &n, &k);
for(int i = 1; i <= n; i++ ){
scanf("%d", &a[i]);
if( a[i] ) e[a[i]].push_back( i );
}
solve();
return 0;
}
H - Hardest Challenge
折半 + 枚举
- 两个人玩游戏,每人有长度相同的三个字符串。
- 每人要组成一个新的字符串,字符串的每一位由自己有的三个字符串对应位置的字符中选一个组成。
- 字符串的权值有一个对应的计算公式,要求权值尽可能的小,问两人谁获胜。
求最小值有一个最麻烦的地方是取模之后的最小值,所以贪心无法完成。
枚举所有的情况是3^28复杂度,血T。
这时候我们考虑将字符串拆成两部分,分别暴力求出3^14种权值和的集合,然后进行两两配对。答案会出现两种情况:
1)两个集合最小值的和
2)两集合选择的权值和刚好大于MOD,由于所有数都小于MOD,所以两个集合分别从大和从小开始枚举,只需要考虑二者和恰好大于等于MOD的边界情况,就类似于尺取想法的两个指针分别移动即可。
P.s. 题面的公式有误,公告区有提及,但题面未修改,正确公式为
$$ Score(S)=( \Sigma^n_{i=1} val \langle S[i] \rangle * 127^{n-i} ) \% MOD $$
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f;
const ll mod = 1e15+37;
int A, B;
char a[3][30], b[3][30];
ll pow127[35];
vector<ll>x, y;
ll ansa = INFLL, ansb = INFLL;
ll quick_pow( ll a, ll b ){
ll res = 1;
while( b ){
if( b&1 ) res = res*a%mod;
a = a*a%mod;
b >>= 1;
}
return res;
}
void init(){
pow127[0] = 1;
for(int i = 1; i < 30; i++ ){
pow127[i] = pow127[i-1]*127%mod;
}
}
void dfs( int A, vector<ll>&x, char a[3][30], int u, int v, ll now ){
for(int i = 0; i < 3; i++ ){
ll tmp = (now+a[i][u]*pow127[A-u])%mod;
if( u == v ){
x.push_back( tmp );
continue;
}
dfs( A, x, a, u+1, v, tmp );
}
}
void get( int A, char a[3][30], ll &ansa )
{
if( A == 1 ){
ansa = min(min(a[0][1]*pow127[0]%mod, a[1][1]*pow127[0]%mod), a[2][1]*pow127[0]%mod );
return;
}
x.clear();
y.clear();
dfs( A, x, a, 1, A/2, 0 );
dfs( A, y, a, A/2+1, A, 0 );
sort( x.begin(), x.end() );
sort( y.begin(), y.end() );
ansa = (x[0]+y[0])%mod;
int j = y.size()-1;
for(int i = 0; i < x.size(); i++ ){
while( j && x[i]+y[j-1] >= mod ) j--;
ansa = min( ansa, (x[i]+y[j])%mod );
}
}
void solve()
{
get( A, a, ansa );
get( B, b, ansb );
if( ansa == ansb ) printf("Tie\n");
else if( ansa < ansb ) printf("Owls\n");
else printf("Goats\n");
}
int main(int argc, char * argv[])
{
init();
scanf("%d %d", &A, &B);
for(int i = 0; i < 3; i++ ){
scanf("%s", &a[i][1] );
}
for(int i = 0; i < 3; i++ ){
scanf("%s", &b[i][1] );
}
solve();
return 0;
}
I - Integer Prefix
签到题
- 输出字符串中从头开始的数字
- 若字符串第一个字符非数字,则输出-1
/*
* @Author: Minisam
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
char s[200010];
int main(){
scanf("%s",s);
if (s[0]<'0' || s[0]>'9') printf("-1\n");
else{
int len = strlen(s);
for (int i=0;i<len;i++){
if (s[i]>='0' && s[i]<='9') printf("%c",s[i]);
else break;
}
printf("\n");
}
return 0;
}
J - Jail Destruction
线段树
- 有n堵墙围成一个环形,高度不一
- 每次操作是,使连续的一段墙面下降,若墙高度为0,则不再下降
- 每次询问是一段区间的墙面和为多少
区间修改,区间查询,所以套线段树即可。
这里唯一难点是下降到0之后不再下降。所以我们引入两个变量记录区间墙的数量,以及区间墙的最低高度,如果有存在操作使最低墙面下降为0,则push_down,一直到底即可。
还有一种可能更省时的方法是,只在查询操作的时候进行push_down操作,但是前者并没有Tle,所以没有修改。
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
#define ls (rt<<1)
#define rs (rt<<1|1)
const int INF = 0x3f3f3f3f;
const int MAXN = 100000+10;
int n, q;
ll a[MAXN];
struct Tree{
int l, r;
int num;
ll mi;
ll res;
ll lz;
}t[MAXN<<3];
void push_up( int rt ){
t[rt].num = t[ls].num + t[rs].num;
t[rt].res = t[ls].res + t[rs].res;
t[rt].mi = min( t[rs].mi, t[ls].mi );
}
void build( int l, int r, int rt ){
t[rt].l = l; t[rt].r = r;
if( l == r ){
t[rt].mi = a[l];
t[rt].res = a[l];
if( a[l] ) t[rt].num = 1;
return;
}
int mid = (l+r)>>1;
build( l, mid, ls );
build( mid+1, r, rs );
push_up( rt );
}
void push_down( int rt ){
t[ls].mi -= t[rt].lz;
t[rs].mi -= t[rt].lz;
t[ls].res -= t[rt].lz*t[ls].num;
t[rs].res -= t[rt].lz*t[rs].num;
if( t[ls].l != t[ls].r ) t[ls].lz += t[rt].lz;
if( t[rs].l != t[rs].r ) t[rs].lz += t[rt].lz;
t[rt].lz = 0;
}
void update( int l, int r, ll x, int rt ){
if( t[rt].num == 0 ) return;
if( l <= t[rt].l && r >= t[rt].r && t[rt].mi >= x ){
t[rt].mi -= x;
t[rt].res -= x*t[rt].num;
t[rt].lz += x;
return;
}
if( t[rt].l == t[rt].r && t[rt].mi <= x ){
t[rt].mi = INF;
t[rt].res = 0;
t[rt].num = 0;
return;
}
if( t[rt].lz ) push_down( rt );
int mid = (t[rt].l+t[rt].r)>>1;
if( mid >= r ) update( l, r, x, ls );
else if( mid < l ) update( l, r, x, rs );
else{
update( l, r, x, ls );
update( l, r, x, rs );
}
push_up( rt );
}
ll query( int l, int r, int rt ){
if( l <= t[rt].l && r >= t[rt].r ){
return t[rt].res;
}
if( t[rt].lz ) push_down( rt );
int mid = (t[rt].l+t[rt].r)>>1;
if( mid >= r ) return query( l, r, ls );
else if( mid < l ) return query( l, r, rs );
else{
return query( l, r, ls )+query( l, r, rs );
}
}
void solve()
{
int x, y;
ll p;
build( 1, n, 1 );
int op;
while( q-- ){
scanf("%d", &op);
if( op == 1 ){
scanf("%d %d", &x, &y);
if( x > y ) printf("%lld\n", query(x,n,1)+query(1,y,1) );
else printf("%lld\n", query(x,y,1) );
}else{
scanf("%d %d %lld", &x, &y, &p);
if( x > y ) { update(x,n,p,1); update(1,y,p,1); }
else update(x,y,p,1);
}
}
}
int main(int argc, char * argv[])
{
scanf("%d %d", &n, &q);
for(int i = 1; i <= n; i++ ){
scanf("%lld", &a[i]);
}
solve();
return 0;
}
K - Kernel Of Love
签到题 思维
- 寻找满足以下条件的pair( x, y )
- x, y 都是 Fibonacci (斐波那契) 数
- gcd( x, y ) = 1
- ( x + y ) mod 2 = 1
- x+y 也是 Fibonacci 数
x+y 也是 Fibonacci 数,则x和y一定是相邻的 Fibonacci ,除了F1 = 1, F3 = 2
相邻的斐波那契数一定互质
斐波那契数列的奇偶序列:两奇一偶
或者简单点打表找规律即可
/*
* @Author: Minisam
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
int f[100010],g[100010];
void solve(){
g[1]=1;g[2]=1;g[3]=0;
f[1]=0;f[2]=0;f[3]=2;
for (int i=4;i<=100000;i++){
g[i]=(g[i-1]+g[i-2])%2;
if (g[i] + g[i-1]== 1) f[i]=f[i-1]+1;
else f[i]=f[i-1];
}
}
int main(){
int T,n;
solve();
scanf("%d",&T);
while (T--){
scanf("%d",&n);
printf("%d\n",f[n]);
}
return 0;
}
L - Liquid X
交互题 + 二分
- 给出n种重量不同的砝码无数个,测量一个未知物体的重量
- 每次由天平可知当前称量的砝码重量轻了or重了
- 尽量少的称量次数称出重量,如果不能则输出-1
这种交互题,很容易想到二分。但本题需要解决两个问题。
1)如何把一个重量拆分成不同重量砝码的重量。1e6*100的数组会mle,所以我们只记录当前重量从哪个重量添加一个砝码得来,由差值得添加砝码的重量。
2)二分得来的重量并不一定能拆分成砝码重量的和,即不能进行称量的重量。所以我们把所有能称量得到的重量放入vector容器,对其进行二分操作。
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define mp(x,y) make_pair(x,y)
const double eps = 1e-9;
const double PI = acos(-1);
const int INF = 0x3f3f3f3f;
const int MAXN = 1000000;
int n;
int green = 0, red = MAXN+1;
int a[105], cnt[105];
int pre[MAXN+10], id[MAXN+10];
char s[20];
vector<int>v;
void init()
{
mss(pre);
queue<int>q;
q.push(0);
while( !q.empty() ){
int now = q.front();
q.pop();
for(int i = 1; i <= n; i++ ){
int to = now+a[i];
if( to > MAXN || pre[to] != -1 ) continue;
pre[to] = now;
q.push( to );
}
}
for(int i = 1; i <= MAXN; i++ ){
if( pre[i] == -1 ) continue;
v.push_back( i );
}
}
int check( int x ){
int y = x;
ms( cnt );
while( x ){
cnt[id[x-pre[x]]]++;
x = pre[x];
}
printf("1\n");
for(int i = 1; i <= n; i++ ){
if( i != 1 ) printf(" ");
printf("%d", cnt[i]);
}
printf("\n");
fflush(stdout);
scanf("%s", s);
if( s[0] == 'y' ) return 2;
else if( s[0] == 'g' ){
green = y;
return 0;
}else{
red = y;
return 1;
}
}
void solve()
{
int l = 0, r = v.size()-1;
int ans = 0;
while( l <= r ){
int mid = (l+r)>>1;
int res = check(v[mid]);
if( res == 2 ){
ans = v[mid];
break;
}else if( res == 1 ){
r = mid-1;
}else{
l = mid+1;
}
}
printf("2\n");
if( ans ){
printf("%d\n", ans);
}else{
if( red-green == 2 ){
printf("%d\n", green+1);
}else{
printf("-1\n");
}
}
fflush(stdout);
}
int main(int argc, char * argv[])
{
scanf("%d", &n);
for(int i = 1; i <= n; i++ ){
scanf("%d", &a[i]);
id[a[i]] = i;
}
init();
solve();
return 0;
}

3 comments
作者的布局谋篇匠心独运,让读者在阅读中享受到了思维的乐趣。
独特的构思和新颖的观点,让这篇文章在众多作品中脱颖而出。
《带我回家2019》剧情片高清在线免费观看:https://www.jgz518.com/xingkong/150843.html