2019-2020 ACM-ICPC Brazil Subregional Programming Contest
A - Artwork
图论
- n×m 的格点图,图上有k个圆
- 问是否可以不经过任何圆的范围从(0,0)到(n,m)
如下方法建图
共 k+4 个点,每相交的圆之间建边,与边界相交的圆也与边界建边
如果图上存在一条通路 左边界->右边界 or 上边界->下边界 or 左边界->下边界 or 上边界->右边界
则从左下到右上的路线会被阻隔,即无法通行
所以 DFS or BFS 判断上述条件即可
/*
* @Author: Minisam
* @School: BIT
*/
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 10010
#define MAXK 1010
using namespace std;
int n,m,k;
int head[MAXK*2]={0};
struct monitor{
double x,y,r;
}a[MAXK];
struct edge{
int to,nxt;
}e[MAXK*MAXK*4];
int ecnt=0;
void addedge(int x,int y){
e[++ecnt].to=y;
e[ecnt].nxt=head[x];
head[x]=ecnt;
e[++ecnt].to=x;
e[ecnt].nxt=head[y];
head[y]=ecnt;
return;
}
int vis[MAXK*2];
int main(){
scanf("%d%d%d",&n,&m,&k);
for (int i=1;i<=k;i++){
scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].r);
}
for (int i=1;i<=k;i++){
for (int j=i+1;j<=k;j++){
if ((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y)<=(a[i].r+a[j].r)*(a[i].r+a[j].r)){
addedge(i,j);
}
}
// left k+1
if (a[i].x<=a[i].r) addedge(i,k+1);
// down k+2
if (a[i].y<=a[i].r) addedge(i,k+2);
// right k+3
if (n-a[i].x<=a[i].r) addedge(i,k+3);
// up k+4
if (m-a[i].y<=a[i].r) addedge(i,k+4);
}
queue<int > Q;
memset(vis,0,sizeof(vis));
vis[k+1]=1;
Q.push(k+1);
int flag=1;
while (!Q.empty()){
int u=Q.front();Q.pop();
for (int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if (v==k+2 || v==k+3) {
flag=0;
break;
}
if(vis[v]==0) {
vis[v]=1;
Q.push(v);
}
}
}
if (!flag) printf("N\n");
else{
while (!Q.empty()) Q.pop();
memset(vis,0,sizeof(vis));
vis[k+4]=1;
Q.push(k+4);
while (!Q.empty()){
int u=Q.front();Q.pop();
for (int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if (v==k+2 || v==k+3){
flag=0;
break;
}
if (vis[v]==0){
vis[v]=1;
Q.push(v);
}
}
}
if (!flag) printf("N\n");
else printf("S\n");
}
return 0;
}
B - Buffoon
签到题
- n个数,判断第一个是否是最大值。
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <bitset>
#include <list>
#include <iomanip>
#include <numeric>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f;
const ll INFLL = 0x3f3f3f3f3f3f3f3f;
#define LOCAL
const int MAXN = 10000+10;
int n;
int a[MAXN];
void solve()
{
for(int i = 1; i <= n; i++ ){
scanf("%d", &a[i]);
}
int flag = 0;
for(int i = 2; i <= n; i++ ){
if( a[i] > a[1] ){
flag = 1;
break;
}
}
if( flag ) printf("N\n");
else printf("S\n");
}
int main(int argc, char * argv[])
{
scanf("%d", &n);
solve();
return 0;
}
C - Crossings With Danger
不会做T_T
D - Denouncing Mafia
DFS + 优先队列
- 一棵树,选取k个点
- 每选取一个点,将该点到根节点路径上的点加入集合
- 使集合Max(size)
DFS求所有节点的最大深度,以及最大深度的走向
根节点的所有子节点用堆维护最大深度
每次删除堆顶子节点的最大深度路径
删除时将非答案路径的支链连到根节点,即加入堆即可
/*
* @Author: Roark
* @School: BIT
*/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<time.h>
#include<climits>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long LL;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int gcd(int a, int b)
{
return b?gcd(b,a%b):a;
}
int head[MAXN];
int all;
struct node
{
int to,nxt;
}e[MAXN<<1];
int deep[MAXN],son[MAXN];
struct Node
{
int u;
int dep;
Node(){}
Node(int u, int dep) : u(u), dep(dep) {}
};
struct cmp{
bool operator()( Node a, Node b ){
return a.dep < b.dep;
}
};
priority_queue<Node, vector<Node>, cmp > big;
void add(int a, int b)
{
e[all].to=b;
e[all].nxt=head[a];
head[a]=all++;
}
void dfs(int u)
{
int mx=0;
for(int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
dfs(v);
if(mx<deep[v])
{
mx=deep[v];
son[u]=v;
}
}
deep[u]=mx+1;
}
void DFS(int u)
{
if(!son[u]) return ;
for(int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
if(v==son[u]) continue;
big.push(Node(v,deep[v]));
}
DFS(son[u]);
}
void init()
{
memset(head,-1,sizeof(head));
all=0;
}
void solve()
{
init();
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n-1;i++)
{
int x;
scanf("%d",&x);
add(x,i+1);
}
int ans=0;
dfs(1);
for(int i=head[1];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
big.push(Node(v,deep[v]));
}
for(int i=1;i<=k;i++)
{
Node top=big.top();
big.pop();
ans+=top.dep;
DFS(top.u);
}
printf("%d\n",ans+1);
}
int main()
{
solve();
return 0;
}
E - Exhibition of Clownfish
不会做T_T
F - Forests in Danger
二分 + 矩形求交(几何) + 矩形求并(扫描线&线段树)
- n条线段,1个矩形
- 问最小的r,使得n条线段向外扩展r的矩形能覆盖指定矩形的面积大于等于指定矩形的p%
- 扩展方法如图

矩形求交 —— 几何求交
Rectangle Intersection( Rectangle a, Rectangle b ){
int X1 = max( a.x1, b.x1 );
int X2 = min( a.x2, b.x2 );
int Y1 = max( a.y1, b.y1 );
int Y2 = min( a.y2, b.y2 );
if( X1 > X2 || Y1 > Y2 ){ //矩形无交
X2 = X1;
Y2 = Y1; // 把矩形变为一个点
}
return Rectangle( X1, Y1, X2, Y2 );
}
矩形求并 —— 扫描线+线段树
可以参考黄学长的博客:http://hzwer.com/879.html
简单点儿说就是,相当于一层一层向上扫描即可,计算每一层的覆盖面积,用线段树维护
具体参考代码
另外二分判断r是否成立即可
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <list>
#include <iomanip>
#include <numeric>
#include <bitset>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define mp(x,y) make_pair(x,y)
#define ls (rt<<1)
#define rs (rt<<1|1)
const double eps = 1e-9;
const double PI = acos(-1);
const int INF = 0x3f3f3f3f;
const int MAXN = 10000+10;
const int MAXM = 100000+10;
int n, p;
int x1[MAXN], x2[MAXN], y_1[MAXN], y2[MAXN];
int X1, X2, Y1, Y2;
struct Tree{
int l, r;
int len;
int cnt;
}t[MAXM<<3];
void build( int l, int r, int rt ){
t[rt].l = l; t[rt].r = r;
t[rt].len = 0;
t[rt].cnt = 0;
if( l == r ){
return;
}
int mid = (l+r)>>1;
build( l, mid, ls );
build( mid+1, r, rs );
}
void push_up( int rt ){
if( t[rt].l == t[rt].r ){
if( t[rt].cnt ) t[rt].len = 1;
else t[rt].len = 0;
return;
}
if( t[rt].cnt ) t[rt].len = t[rt].r-t[rt].l+1;
else t[rt].len = t[ls].len+t[rs].len;
}
void update( int l, int r, int w, int rt ){
if( t[rt].l >= l && t[rt].r <= r ){
t[rt].cnt += w;
push_up( rt );
return;
}
int mid = (t[rt].l+t[rt].r)>>1;
if( mid < l ) update( l, r, w, rs );
else if( mid >= r ) update( l, r, w, ls );
else{
update( l, r, w, ls );
update( l, r, w, rs );
}
push_up( rt );
}
struct node{
int x[2], y;
int op;
node(){
node( int _x1, int _x2, int _y, int _op ){
x[0] = _x1; x[1] = _x2; y = _y; op = _op;
}
bool operator<( const node &b ) const {
if( y == b.y ) return op > b.op;
return y < b.y;
}
}e[MAXN<<1];
bool check( int r ){
for(int i = 1; i <= n; i++ ){
int xx1 = max( X1, x1[i]-r );
int xx2 = min( X2, x2[i]+r );
int yy1 = max( Y1, y_1[i]-r );
int yy2 = min( Y2, y2[i]+r );
if( yy2 < yy1 ) yy2 = yy1;
if( xx2 < xx1 ) xx2 = xx1;
e[2*i-1] = node( xx1-X1, xx2-X1, yy1-Y1, 1 );
e[2*i] = node( xx1-X1, xx2-X1, yy2-Y1, -1 );
}
sort( e+1, e+2*n+1 );
build( 1, X2-X1, 1 );
int Len = 0, y = 0;
ll S = 0;
for(int i = 1; i <= 2*n; i++ ){
if( e[i].x[1] <= e[i].x[0] ) continue;
S += 1ll*Len*(e[i].y-y);
y = e[i].y;
update( e[i].x[0]+1, e[i].x[1], e[i].op, 1 );
Len = t[1].len;
}
if( S*100 >= 1ll*(X2-X1)*(Y2-Y1)*p ) return 1;
else return 0;
}
void solve()
{
int ans = 100000;
int l = 0, r = 100000;
while( l <= r ){
int mid = (l+r)>>1;
if( check(mid) ){
ans = mid;
r = mid-1;
}else{
l = mid+1;
}
}
printf("%d\n", ans);
}
int main(int argc, char * argv[])
{
scanf("%d", &n);
for( int i = 1; i <= n; i++ ){
scanf("%d %d %d %d", &x1[i], &y_1[i], &x2[i], &y2[i] );
if( x1[i] > x2[i] ) swap( x1[i], x2[i] );
if( y_1[i] > y2[i] ) swap( y_1[i], y2[i] );
}
scanf("%d", &p);
scanf("%d %d %d %d", &X1, &Y1, &X2, &Y2);
solve();
return 0;
}
G - Getting Confidence
最小费用最大流 or KM
- n个任务,n个人,给出每个人完成每种任务的权值
- 求最大权值的乘积
经典的任务分配问题,用最小费用最大流或KM解决
其中需要把乘积转换为加法,所以对权值取对数
计算最小费用,所以将所有权值取负
/*
* @Author: Roark
* @School: BIT
*/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<time.h>
#include<climits>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long ll;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 100 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const int N = 500 + 10;
const int M = 30000 + 10;
ll read()
{
ll x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-')f = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int n;
struct Edge
{
int from, to, next, cap;
double cost;
Edge() {}
Edge(int from, int to, int next, int cap, double cost) :
from(from), to(to), next(next), cap(cap), cost(cost) {}
} edge[M];
int head[N], tot;
void add(int from, int to, int cap, double cost)
{
edge[tot] = Edge(from, to, head[from], cap, cost);
head[from] = tot++;
edge[tot] = Edge(to, from, head[to], 0, -cost);
head[to] = tot++;
}
void init()
{
memset(head,-1, sizeof(head));
tot = 0;
}
double dis[N];
int pre[N];
bool vis[N];
queue<int> q;
bool spfa(int s, int t)
{
while (!q.empty()) q.pop();
for(int i = 0; i <= 2*n+2; i++ ){
dis[i] = 100000;
}
memset(vis, false, sizeof(vis));
memset(pre,-1, sizeof(pre));
q.push(s); vis[s] = true; dis[s] = 0;
while (!q.empty())
{
int u = q.front(); q.pop(); vis[u] = false;
for (int i = head[u]; i != -1; i = edge[i].next){
if (edge[i].cap && dis[u] + edge[i].cost < dis[edge[i].to])
{
int v = edge[i].to;
dis[v] = dis[u] + edge[i].cost;
pre[v] = i;
if (!vis[v]) q.push(v), vis[v] = true;
}
}
}
return dis[t] < 0;
}
double mcmf(int s, int t, int& maxflow)
{
double mincost = 0;
maxflow = 0;
while (spfa(s, t))
{
int flow = INF;
for (int i = pre[t]; i != -1; i = pre[edge[i].from])
flow = min(flow, edge[i].cap);
for (int i = pre[t]; i != -1; i = pre[edge[i].from])
{
edge[i].cap -= flow;
edge[i ^ 1].cap += flow;
mincost += edge[i].cost;
}
maxflow += flow;
}
return mincost;
}
int ans[100 + 10];
double happy[MAXN][MAXN];
int main()
{
scanf("%d", &n);
init();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int x;
scanf("%d",&x);
happy[i][j]=log(x);
}
}
for(int i=1;i<=n;i++)
{
add(2*n+1,i,1,0);
}
for(int i=1;i<=n;i++)
{
add(i+n,2*n+2,1,0);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
add(i,n+j,1,-happy[i][j]);
}
}
int maxflow;
double mincost = mcmf(2*n+1, 2*n+2, maxflow);
for(int i=1;i<=n;i++)
{
for(int j=head[i];j!=-1;j=edge[j].next)
{
if(edge[j].cap==0)
{
ans[edge[j].to-n]=edge[j].from;
}
}
}
for(int i=1;i<=n;i++)
{
if(i!=1) printf(" ");
printf("%d",ans[i]);
}
printf("\n");
return 0;
}
H - Hour for a Run
签到题
- 计算 n*v 的 10%,20% ... 90%,分别向上取整的值
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <bitset>
#include <list>
#include <iomanip>
#include <numeric>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f;
const ll INFLL = 0x3f3f3f3f3f3f3f3f;
#define LOCAL
int n, v;
void solve()
{
for( int i = 1; i <= 9; i++ ){
if( i != 1 ) printf(" ");
printf("%d", (v*n*i+9)/10);
}
printf("\n");
}
int main(int argc, char * argv[])
{
scanf("%d %d", &v, &n);
solve();
return 0;
}
I - Interplanetary
特殊的最短路 - Floyd
- 一共n个星球,每个星球有对应的温度
- 共m条带权双向边连接星球,构成一张图
- 共q组询问
- 每组询问从a到b星球的最短路,并要求途经的星球必须是所有星球温度最高(最低)的k个
离线处理,将询问分为要求温度最高和最低的两种
两种分别建图,用Floyd跑最短路
在跑最短路的同时,根据星球温度的高低一次添加点
如果当前星球温度不符合当前询问的要求,先处理当前询问,再继续添点
所以需要将星球和询问都按温度高低进行排序
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <list>
#include <iomanip>
#include <numeric>
#include <bitset>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define msss(s) memset(s, INF, sizeof(s))
#define mp(x,y) make_pair(x,y)
const double eps = 1e-9;
const double PI = acos(-1);
const int INF = 0x3f3f3f3f;
const int MAXN = 400+5;
const int MAXQ = 1e5+10;
int n, m, q;
int ans[MAXQ];
int e[2][MAXN][MAXN];
struct node{
int t, id, p[2];
}a[MAXN];
bool cmp( node a, node b ){
return a.t < b.t;
}
struct query{
int u, v, k, id;
query(){}
query( int u, int v, int k, int id ) : u(u), v(v), k(k), id(id) {}
bool operator < ( const query &b ) const {
return k < b.k;
}
};
vector<query>V[2];
vector<query>:: iterator it;
void floyd( int op ){
it = V[op].begin();
for( int l = 1; l <= n; l++ ){
int p;
if( op ) p = n-l+1;
else p = l;
for( int i = 1; i <= n; i++ ){
for( int j = 1; j <= n; j++ ){
e[op][i][j] = min( e[op][i][j], e[op][i][a[p].id]+e[op][a[p].id][j] );
}
}
int nxtp;
if( op ) nxtp = p-1;
else nxtp = p+1;
while( it != V[op].end() && a[nxtp].p[op] > (*it).k ){
ans[(*it).id] = e[op][(*it).u][(*it).v];
it++;
}
}
}
void solve()
{
sort( a+1, a+n+1, cmp );
a[0].t = -INF;
a[n+1].t = INF;
int tmp = 0;
for(int i = 1; i <= n; i++ ){
if( a[i].t == a[i-1].t ){
a[i].p[0] = tmp;
}else{
a[i].p[0] = ++tmp;
}
}
a[0].p[0] = 0;
a[n+1].p[0] = n+1;
tmp = 0;
for(int i = n; i >= 1; i-- ){
if( a[i].t == a[i+1].t ){
a[i].p[1] = tmp;
}else{
a[i].p[1] = ++tmp;
}
}
a[0].p[1] = n+1;
a[n+1].p[1] = 0;
floyd( 0 );
floyd( 1 );
for( int i = 1; i <= q; i++ ){
if( ans[i] == INF ) printf("-1\n");
else printf("%d\n", ans[i]);
}
}
int main(int argc, char * argv[])
{
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++ ){
scanf("%d", &a[i].t);
a[i].id = i;
}
msss( e );
for(int i = 1; i <= n; i++ ){
e[0][i][i] = e[1][i][i] = 0;
}
int x, y, w;
while( m-- ){
scanf("%d %d %d", &x, &y, &w);
e[0][x][y] = e[1][x][y] = w;
e[0][y][x] = e[1][y][x] = w;
}
scanf("%d", &q);
int u, v, k, op;
for(int i = 1; i <= q; i++ ){
scanf("%d %d %d %d", &u, &v, &k, &op);
if( op ){
V[1].push_back( query( u, v, k, i ) );
}else{
V[0].push_back( query( u, v, k, i ) );
}
}
sort( V[1].begin(), V[1].end() );
sort( V[0].begin(), V[0].end() );
solve();
return 0;
}
J - Jar of Water Game
模拟
- 一种卡牌游戏
- n个人围成一圈
- 有n种牌型,每个牌型4张牌
- 每个人初始有4张牌
- 有一张wildcard,并会在游戏开始时把牌交给一个人,且他成为第一个出牌的人
- 每个人按顺序依次选择手中的一张牌将其交给下家
- 如果此时玩家有wildcard,会选择wildcard,除非他是刚获得wildcard(即刚获得wildcard的出牌轮不能选择wildcard)
- 其他时候会选择手中牌型数最少的牌型,如果有相同的,选择牌价值更小的出牌
- 当有玩家仅有4张牌,且4张牌牌型相同,并不包含wildcard时获胜
- 如果有多人满足获胜条件,则牌价值更小者获胜
就纯暴力模拟就好了
有一个小Trick,就是牌价值排序不符合斗地主,也不符合正常卡牌游戏
从低到高依次是A23456789DQJK,就QJK很难受,队友看了一个小时看不出来问题在哪
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <list>
#include <iomanip>
#include <numeric>
#include <bitset>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define mp(x,y) make_pair(x,y)
const double eps = 1e-9;
const double PI = acos(-1);
const int INF = 0x3f3f3f3f;
int card[20][20];
int wild[20];
int n, k;
char s[10];
bool win(){
int wi = 0, wi_num = INF;
for( int i = 1; i <= n; i++ ){
if( wild[i] ) continue;
int all = 0;
int flag = 0;
for( int j = 1; j <= 13; j++ ){
all += card[i][j];
if( card[i][j] == 4 ) flag = j;
}
if( all == 4 && flag ){
if( flag < wi_num ){
wi_num = flag;
wi = i;
}
}
}
if( wi ){
printf("%d\n", wi);
return 1;
}else return 0;
}
int count( int x ){
int cnt = INF;
int num = 0;
for( int i = 1; i <= 13; i++ ){
if( card[x][i] && card[x][i] < cnt ){
cnt = card[x][i];
num = i;
}
}
return num;
}
void solve()
{
int cur = k;
int round = 1;
while( 1 ){
if( win() ) break;
int nxt = cur%n+1;
if( wild[cur] == 1 ){
wild[cur] = 0;
wild[nxt] = 2;
cur = nxt;
continue;
}
if( wild[cur] == 2 ){
wild[cur] = 1;
}
int w = count( cur );
card[cur][w]--;
card[nxt][w]++;
cur = nxt;
}
}
int main(int argc, char * argv[])
{
scanf("%d %d", &n, &k);
for(int i = 1; i <= n; i++ ){
scanf("%s", s);
for(int j = 0; j < 4; j++ ){
if( s[j] == 'A' ) card[i][1]++;
else if( s[j] == 'D' ) card[i][10]++;
else if( s[j] == 'Q' ) card[i][11]++;
else if( s[j] == 'J' ) card[i][12]++;
else if( s[j] == 'K' ) card[i][13]++;
else card[i][s[j]-'0']++;
}
}
wild[k] = 2;
solve();
return 0;
}
K - Keep Calm and Sell Balloons
递推&DP + 矩阵快速幂
- 2*n的格子
- 任意选定起点和终点
- 每次可以走周围8个格子,即上、下、左、右、左上、左下、右上、右下
- 问不重复走完所有格子的方案数
很容易想到n具有递推关系
可以将结尾的两个格子进行分类,共分成四类如下
第一类:两格子相连,不包含起点终点
第二类:两格子相连,且其中一点为起点或终点
第三类:两格子不相连,且其中一点为起点或终点
第四类:两格子不相连,且都为起点终点
例如n=2时,四类分别如图:(每个图对应两个方向,即两种情况)
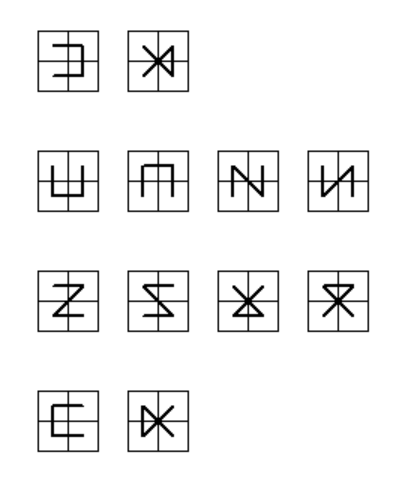
所以可以求出递推公式为:
$$ x1_{i+1} = 2*x1_i + 2*x2_i $$
$$ x2_{i+1} = 2*x2_i + 2*x3_i + 4*x4_i $$
$$ x3_{i+1} = 2*x2_i $$
$$ x4_{i+1} = 2*x4_i $$
递推公式很容易想到,用矩阵快速幂即可
/*
* @Author: DarkDawn
* @School: BIT
*/
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <bitset>
#include <list>
#include <iomanip>
#include <numeric>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
#define mss(s) memset(s, -1, sizeof(s))
#define PI acos(-1)
#define eps 1e-9
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f;
const ll INFLL = 0x3f3f3f3f3f3f3f3f;
#define LOCAL
const ll mod = 1e9+7;
int n;
struct Matrix{
ll M[4][4];
void init(){
ms( M );
for(int i = 0; i < 4; i++ ){
M[i][i] = 1;
}
}
Matrix operator *( Matrix &b ){
Matrix c;
ms( c.M );
for(int i = 0; i < 4; i++ ){
for(int j = 0; j < 4; j++ ){
for(int k = 0; k < 4; k++ ){
c.M[i][j] += M[i][k]*b.M[k][j]%mod;
}
c.M[i][j] %= mod;
}
}
return c;
}
}a, b;
void quickpow( int n ){
while( n ){
if( n&1 ) a = a*b;
b = b*b;
n >>= 1;
}
}
void solve()
{
if( n == 1 ){
printf("2\n");
return;
}
n -= 2;
a.M[0][0] = 2;
a.M[0][1] = 4;
a.M[0][2] = 4;
a.M[0][3] = 2;
b.M[0][0] = 2;
b.M[1][0] = 2;
b.M[1][1] = 2;
b.M[1][2] = 2;
b.M[2][1] = 2;
b.M[3][1] = 4;
b.M[3][3] = 2;
quickpow( n );
ll ans = 0;
for(int i = 0; i < 4; i++ ){
ans += a.M[0][i];
}
ans = ans*2%mod;
printf("%lld\n", ans);
}
int main(int argc, char * argv[])
{
scanf("%d", &n);
solve();
return 0;
}
L - Less Coin Tosses
找规律
- 问长度为 n 的 01 串最多能均分多少
- 均分标准为每两个串满足0和1的个数相等,就分开
- 问最少剩余多少个串
问题可以抽象为如下表达式
$$ \sum_{i=0}^n C_n^i mod 2 $$
打个表找规律可以发现
将 n 转化为二进制,有几个1,答案就是2的几次方
/*
* @Author: Minisam
* @School: BIT
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long int
using namespace std;
LL n;
int main(){
scanf("%lld",&n);
int x=0;
while (n){
x+=n%2;
n>>=1;
}
printf("%lld",(1ll<<x));
return 0;
}
M - Maratona Brasileira de Popcorn
二分 + 贪心
- 有n袋爆米花,每袋数量给出
- 有c个人吃爆米花,每个人只能吃连续的几袋爆米花,每袋爆米花只能一个人吃
- 所有人吃爆米花的速度都是每秒钟吃t个
- 问最短多长时间吃完爆米花
对总时长进行二分
然后每个人在时间内尽可能多吃,check是否满足条件
/*
* @Author: Roark
* @School: BIT
*/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<time.h>
#include<climits>
using namespace std;
#define fi first
#define se second
#define Chtholly_is_so_cute ios::sync_with_stdio(false);cin.tie(0);
#define pb push_back
#define Max(x,y) (x>y?x:y)
#define Min(x,y) (x<y?x:y)
#define ls (rt<<1)
#define rs (rt<<1|1)
#define debug(x) printf("# %d\n",x)
typedef long long LL;
typedef unsigned long long uLL;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 10;
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int gcd(int a, int b)
{
return b?gcd(b,a%b):a;
}
int a[MAXN];
void solve()
{
int n,m,t;
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
LL ans=0;
LL l=1,r=1000000000;
while(l<=r)
{
LL mid=(l+r)>>1;
LL cnt=1;
LL rem=t*mid;
LL c=0;
for(int i=1;i<=n;i++)
{
if(a[i]>rem)
{
cnt=INF;
break;
}
if(c+a[i]<=rem)
{
c+=a[i];
}
else
{
cnt++;
c=a[i];
}
}
if(cnt>m)
{
l=mid+1;
}
else
{
r=mid-1;
ans=mid;
}
}
printf("%lld\n",ans);
}
int main()
{
solve();
return 0;
}
