TPAMI
摘要
We introduce CAMRL, the first curriculum-based asymmetric multi-task learning (AMTL) algorithm for dealing with multiple reinforcement learning (RL) tasks altogether. To mitigate the negative influence of customizing the one-off training order in curriculum-based AMTL, CAMRL switches its training mode between parallel single-task RL and asymmetric multi-task RL (MTRL), according to an indicator regarding the training time, the overall performance, and the performance gap among tasks. To leverage the multi-sourced prior knowledge flexibly and to reduce negative transfer in AMTL, we customize a composite loss with multiple differentiable ranking functions and optimize the loss through alternating optimization and the Frank-Wolfe algorithm. The uncertainty-based automatic adjustment of hyper-parameters is also applied to eliminate the need of laborious hyper-parameter analysis during optimization. By optimizing the composite loss, CAMRL predicts the next training task and continuously revisits the transfer matrix and network weights. We have conducted experiments on a wide range of benchmarks in multi-task RL, covering Gym-minigrid, Meta-world, Atari video games, vision-based PyBullet tasks, and RLBench, to show the improvements of CAMRL over the corresponding single-task RL algorithm and state-of-the-art MTRL algorithms. The code is available at: https://github.com/huanghanchi/CAMRL
我们介绍了CAMRL,这是第一个基于课程的非对称多任务学习(AMTL)算法,用于完全处理多个强化学习(RL)任务。为了减轻基于课程的AMTL中指定一次性训练顺序的负面影响,CAMRL根据训练时间、整体性能和任务间性能差距的指标,在并行单任务RL和非对称多任务RL(MTRL)之间切换其训练模式。为了灵活地利用多源先验知识并减少AMTL中的负迁移,我们定制了一个复合损失函数,其具有多个可微分排名函数,并通过交替优化和Frank-Wolfe算法进行优化。基于不确定性的超参数自动调整也被应用,以消除优化过程中费力的超参数分析的需要。通过优化综合损失,CAMRL预测下一个训练任务,并不断重新审视传输矩阵和网络权重。我们在多任务RL的各种基准上进行了实验,包括Gym-minigrid、Meta-world、Atari视频游戏、基于视觉的PyBullet任务和RLBench,以显示CAMRL比相应的单任务RL算法和最先进的MTRL算法的改进。
研究动机
- 在MTL中,不是所有的任务都能从联合学习中受益,所以可能会出现负迁移
- 核心想法是通过基于课程的非对称多任务学习(AMTL)模式学习每个两个任务之间的稀疏加权定向正规化图
- 若缺乏对RL任务属性的先验知识,直接采用基于课程的AMTL来逐一训练任务,不当的训练顺序可能导致学到一个糟糕的正则化图
- 现有的关于AMTL的工作忽略了一些重要的因素,如代表相对训练进度的指标,任务之间的转移性能,以及描述行为的多样性,以便灵活地进行任务之间的转移和避免负迁移
主要贡献
- 提出的CAMRL算法主要包含「训练模式转换机制」和「多个可微分排名函数构成的组合损失」
- CAMRL可以与其他RL算法以及训练模式相结合,包括引入先验知识等。通过自动参数调节可以适应新的任务
- 在多个Benchmark上进行了实验
方法描述
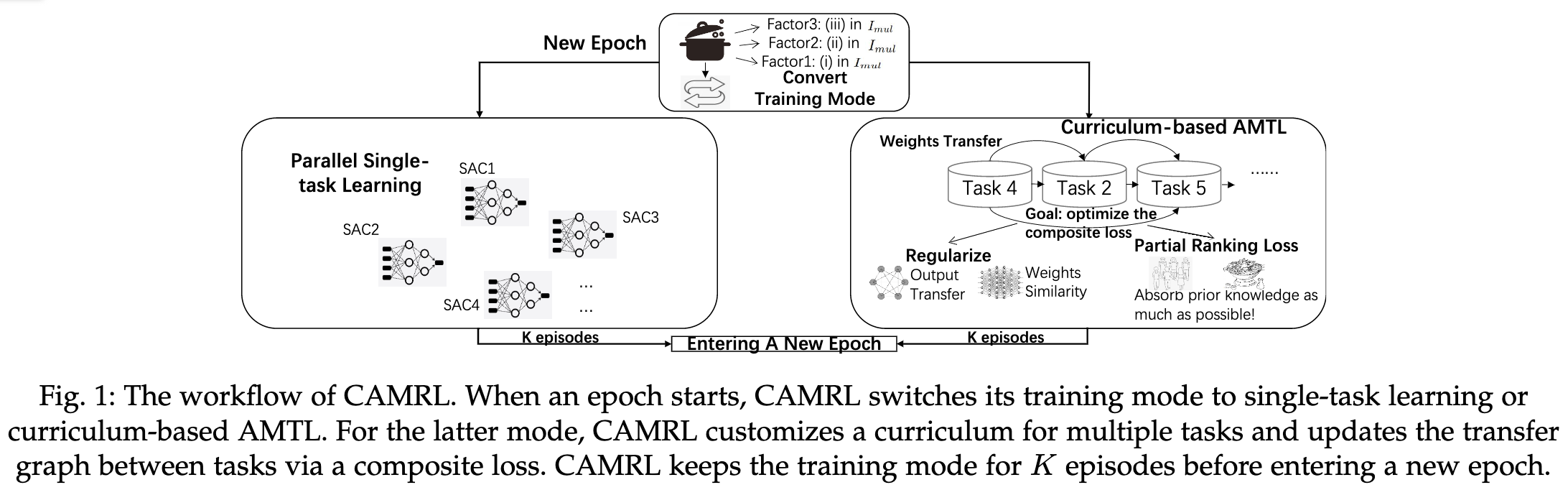
整体架构
- 一个学习进度指标选择训练模式:在每个epoch开始前选择用parallel single-task training or curriculum-based AMTL
- 如果使用curriculum-based AMTL,则使用一个综合loss来学习任务迁移
- 使用交替优化和Frank-Wolfe算法来决定下一个训练任务和更新迁移矩阵
- 超参数根据每轮的历史不确定性自动调整
- 当有新任务时,可以通过调整迁移矩阵快速适应

算法解析
- 每个任务 $t \in [T]$ 对应一个独立的SAC网络 $SAC_t$,其网络参数为$w_t$
- 首先独立对每个任务进行N个epoch的训练,各任务互不影响
之后计算指标 $I_{mul} = \frac{(i)+(ii)+(iii)}{3}$ 用于选择下一个epoch的训练模式
(i):$\exp(-n/a)$:为加大在早期进行多任务训练的可能性,以便使难训练的任务尽早受益于易训练的任务
- $n$:当前的epoch数
(ii):$\exp(-\mathcal{L}_{nor}*b)$:如果整体训练表现较差,即$\mathcal{L}_{nor}$较大,则执行任务迁移的可能性往往较小。
- $\mathcal{L}_{nor}=\frac{policy\_loss-average_{policy\_loss}}{std_{policy\_loss}}$:上一个epoch所有任务的平均归一化policy损失
(iii):最后一个epoch的平均归一化奖励不在$[\mathcal{R}_{nor}-c*std_{nor},\mathcal{R}_{nor}+c*std_{nor}]$区间的任务百分比
- $std_{nor}$:所有任务的归一化奖励标准偏差
- 任务之间的学习过程差距越大,执行多任务训练的可能性就越大。
如果 $u \sim Uniform([0,1]) < I_{mul}$ 则暂时在下一个epoch使用curriculum-based AMTL训练;否则使用单任务训练
- ==与算法描述冲突,根据理解,此处描述为正确,算法表示错误==
课程多任务学习
- $B$:一个 $T \times T$ 的矩阵表示任意两个任务之间的迁移数量?
任务 $t$ 的SAC网络参数:$w_t \approx \sum_{s=1}^TB_{st}w_s$
- $B_{st}$:用基础参数 $w_s$ 表示目标参数 $w_t$ 的权重
- $W := (w_1,w_2,\dots,w_T)$
复合损失函数:$\mathcal{L}(W,B)=\sum_{t=1}^T\{(1+mu\|b_t^o\|_1)\mathcal{L}(w_t)+\lambda\|w_t-\sum_{s \neq t}B_{st}w_s\|_2^2\}$
- $b_t^o=(B_{t1},\dots,B_{t(t-1)},B_{t(t+1)},\dots, B_{tT})^\top \in \mathbb{R}^{T-1}$ ,$\|b_t^o\|_1$ 表示任务 $t$ 迁移到其他任务的稀疏度计数
- $\mathcal{L}(w_t)$ 表示任务 $t$ 在权重 $w_t$ 下计算的SAC policy loss
- $(\lambda,\mu)$ 为两个权重超参数
考虑课程学习的损失函数:$\min _{\pi \in \mathcal{S}, W, B \geq 0} \sum_{i=1}^T\left\{\left(1+\mu\left\|b_{\pi(i)}^o\right\|_1\right) \mathcal{L}\left(w_{\pi(i)}\right)+\lambda\left\|w_{\pi(i)}-\sum_{j=1}^{i-1} B_{\pi(j) \pi(i)} w_{\pi(j)}\right\|_2^2\right\}$
- 同时优化 $W$ 和 $B$ 可能导致严重的负迁移和维数灾难,所以希望以最佳的顺序依次优化 $b_t^o$ 和 $w_t$
- $\mathcal{S}$ 表示 $T$ 个元素的置换空间;对任意 $\pi \in S$,$\pi(i)$ 表示置换的第 $i$ 个元素
- 令 $\mathcal{T}:= \{\pi(1), \dots, \pi(i-1)\}$ 表示前 $i-1$ 个已经训练的任务;$\mathcal{U} := \{1,\dots,T\}-\mathcal{S}$ 表示还未训练的任务
每次训练在 $\mathcal{U}$ 中选择任务 $t$ 并对 $b_t^o$ 进行训练:$\left(t, b_t^o\right) \leftarrow \underset{t \in \mathcal{U}, b_t^o}{\arg \min }\left\{\left(1+\mu\left\|b_t^o\right\|_1\right) \mathcal{L}\left(w_t\right)+\lambda \sum_{s \in \mathcal{U}-t}\left\|w_s-\sum_{j=1}^{i-1} B_{\pi(j) s} w_{\pi(j)}-B_{t s} w_t\right\|_2^2\right\}$
- 即寻找当下能进行最大程度优化的任务
- 再对 $w_t$ 进行优化:$w_t \leftarrow \underset{w_t}{\arg \min }\left\{\left(1+\mu\left\|b_t^o\right\|_1\right) \mathcal{L}\left(w_t\right)+\lambda\left\|w_t-\sum_{j=1}^{i-1} B_{\pi(j) t} w_{\pi(j)}\right\|_2^2\right\}$
其他Loss设计
- 为合理计数每两个任务之间的迁移,并避免过多的负迁移,提出3个期望,并对应更改损失函数
[Expectation 1]: Ranking Loss 1
如果测试迁移率性能满足 $p_{t,i_1} > p_{t,i_2} > \dots > p_{t,i_q}$,则期望迁移矩阵满足 $B_{t,i_1} > B_{t,i_2} > \dots > B_{t,i_q}$
- $p_{t,i}$:将在任务 $t$ 上训练的网络在任务 $i$ 上测试的平均奖励作为性能指标
- 某任务在其他任务上的评估性能更好,则该任务的迁移数量越大
所以该期望损失表示为最小化 $\sum_{j=1}^q(j-y_{i_j})^2$
- 其中 $j$ 表示 $p_{t,i_j}$ 在 $p_{t,i_1} > p_{t,i_2} > \dots > p_{t,i_q}$ 中的排名;$y_{i_j}$ 表示 $B_{t,i_j}$ 对应的排名
由于 $y_{i_j}$ 不可微分,所以构建了一个可微分排名函数:$y_{i_j}'=q+1-\sum_{s=1}^q\{0.5*\tanh[d(B_{t,i_j}-B_{t,i_s})]+0.5\}$
- 即用一个复合tanh函数构建一个可微的阶梯函数
- 不同超参数 $d$ 生成的函数对应如下
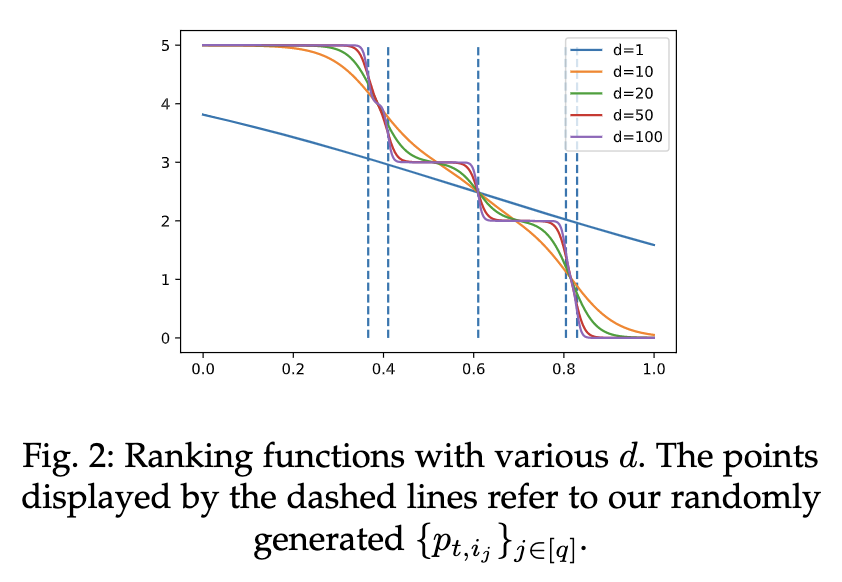
- 性能指标也可以融入其他先验知识或训练指标
- 在每训练 $K$ 个epoch之后随机选择部分任务对性能 $p_{i,j}$ 进行更新
[Expectation 2]: Ranking Loss 2
- 如果任务 $i$ 是easy-to-train(即 $\mathcal{L}(w_i)$ 很小),则期望其不大需要其他任务的迁移
所以该期望损失表示为最小化两项:$ -(b_t^o)^\top l_t^o$ 和 $\sum_{j \in [T]}(rank_j^{(1)}-y''_j)^2$
- 其中 $l_t^o = (\mathcal{L}(w_1),\dots,\mathcal{L}(w_{t-1}),\mathcal{L}(w_{t+1}),\dots,\mathcal{L}(w_T))$;$rank_j^{(1)}$ 表示 $\mathcal{L}(w_j)$ 的排名;$y_j''$ 表示 $B_{t,j}$ 的排名
- 最大化 $(b_t^o)^\top l_t^o$ 即期望 $\mathcal{L}(w_i)$ 大的 $B_{t,i}$ 大,反之亦然;即符合期望2
[Expectation 3]: Ranking Loss 2
- 如果任务 $i$ 和任务 $t$ 很相似,则期望这两个任务间的迁移越大
所以该期望损失表示为最小化 $\sum_{j \in [T]}(rank_j^{(2)}-y''_j)^2$
- 其中 $rank_j^{(2)}$ 表示 $s_{j,t}$ 的排名,$s_{j,t}$ 表示任务 $j$ 和 $t$ 的相似度
相似度计算共提出三种方案
- critic网络的cosine相似度(实验验证该方案最佳)
- policy网络的cosine相似度
状态空间中的embedding负距离
- 计算 $s_{i,j}$ 的具体做法:先采样100个状态;分别使用任务 $i$ 和 $j$ 的embedding层获得向量 $e_{i,1},\dots,e_{i,100}$ 和 $e_{j,1},\dots,e_{j,100}$;最后计算负距离 $-\sqrt{\frac{1}{100} \sum_{m=1}^{100}\left\|e_{i, m}-e_{j, m}\right\|_2^2}$ 表示相似度
所以对于 $b_t^o$ 的训练变更为:
- 先固定 $b_t^o$ 和 $W$ 选择最小化该目标的下一个训练任务 $t$
- 然后固定 $t$ 和 $W$ 使用Frank-Wolfe优化参数 $b_t^o$
- 最后固定 $t$ 和 $b_t^o$ 训练任务 $t$ 的policy参数 $w_t$
$$ \begin{aligned} \left(t, b_t^o\right) & \leftarrow \underset{t \in \mathcal{U}, b_t^o}{\arg \min }\left\{\lambda_0\left[\left(1+\mu_1\left\|b_t^o\right\|_1\right) \mathcal{L}\left(w_t\right)-\mu_2\left(b_t^o\right)^{\top} l_t^o\right]\right. \\ &+\lambda_1 \sum_{s \in \mathcal{U}-t}\left\|w_s-\sum_{j=1}^{i-1} B_{\pi(j) s} w_{\pi(j)}-B_{t s} w_t\right\|_2^2+\lambda_2 \sum_{j \in[q]}\left(j-y i_{i_j}\right)^2 \\ &\left.+\lambda_3 \sum_{j \in[T]}\left(r a n k_j^{(1)}-y \prime_j\right)^2+\lambda_4 \sum_{j \in[T]}\left(r a n k_j^{(2)}-y \prime_j\right)^2\right\} \end{aligned} $$
loss优化
优化 $b_t^o$:为使loss可微以及保证迁移矩阵 $B$ 的稀疏型,用 $\mu_1 \sum_{j \in [T]-\{t\}}B_{tj}$ 代替 $\mu_1\left\|b_t^o\right\|_1$
- 加入限制条件:$b_t^o \ge 0, \quad \|b_t^o\|_1 \le radius < \frac{1}{2}$,其中 $radius$ 是 $\|b_t^o\|_1(t \in [T])$ 的上界
- 所以 $b_t^o$ 的优化函数转化为:$\min _{b_t^o \geq 0,\left\|b_t^o\right\|_1 \leq radius} f\left(b_t^o\right)$
$$ \begin{aligned} f\left(b_t^o\right) & = \lambda_0\left[\left(1+\mu_1 \sum_{j \in [T]-\{t\}}B_{tj}\right) \mathcal{L}\left(w_t\right)-\mu_2\left(b_t^o\right)^{\top} l_t^o\right] \\ &+\lambda_1 \sum_{s \in \mathcal{U}-t}\left\|w_s-\sum_{j=1}^{i-1} B_{\pi(j) s} w_{\pi(j)}-B_{t s} w_t\right\|_2^2+\lambda_2 \sum_{j \in[q]}\left(j-y i_{i_j}\right)^2 \\ &\left.+\lambda_3 \sum_{j \in[T]}\left(r a n k_j^{(1)}-y \prime_j\right)^2+\lambda_4 \sum_{j \in[T]}\left(r a n k_j^{(2)}-y \prime_j\right)^2\right\} \end{aligned} $$
超参数动态调节:根据历史epoch每项对应的标准差自动调节 $\{\lambda_i\}_{i=0}^4$
- 具体表示为:$\lambda_i = \frac{1}{4\sigma_i^0+\epsilon}(i \in [4])$ 和 $\lambda_0 = \frac{1}{2\sigma_0^0+\epsilon}$
- 其中 $\sigma_i$ 表示 $\lambda_i$ 对应项损失的标准差;$\epsilon(=10^{-2})$ 为避免分母为0
- 第0项权重较大是因为其为主要优化目标
理论分析
Convergence of Vanilla Frank-Wolfe Algorithm(==TODO还没仔细看==)
- 对于原式:
$$ \begin{aligned} f\left(b_t^o\right) & = \lambda_0\left[\left(1+\mu_1 \sum_{j \in [T]-\{t\}}B_{tj}\right) \mathcal{L}\left(w_t\right)-\mu_2\left(b_t^o\right)^{\top} l_t^o\right] \\ &+\lambda_1 \sum_{s \in \mathcal{U}-t}\left\|w_s-\sum_{j=1}^{i-1} B_{\pi(j) s} w_{\pi(j)}-B_{t s} w_t\right\|_2^2+\lambda_2 \sum_{j \in[q]}\left(j-y i_{i_j}\right)^2 \\ &\left.+\lambda_3 \sum_{j \in[T]}\left(r a n k_j^{(1)}-y \prime_j\right)^2+\lambda_4 \sum_{j \in[T]}\left(r a n k_j^{(2)}-y \prime_j\right)^2\right\} \end{aligned} $$
- 对于 $\left(1+\mu_1 \sum_{j \in [T]-\{t\}}B_{tj}\right) \mathcal{L}\left(w_t\right)-\mu_2\left(b_t^o\right)^{\top} l_t^o$ 为 $\left(\mu_1+\mu_2\right) D_1T$-Lipschitz
- 对于 $\lambda_1 \sum_{s \in \mathcal{U}-t}\left\|w_s-\sum_{j=1}^{i-1} B_{\pi(j) s} w_{\pi(j)}-B_{t s} w_t\right\|_2^2$ 为 $\lambda_1 D_2^2T$-Lipschitz
- 因为 $[\tanh(x)]'=1-(\tanh(x))^2$,所以对于 $lambda_2 sum_{j in[q]}left(j-y i_{i_j}right)^2
+lambda_3 sum_{j in[T]}left(r a n k_j^{(1)}-y prime_jright)^2+lambda_4 sum_{j in[T]}left(r a n k_j^{(2)}-y prime_jright)^2$ 为 $2left(lambda_2+lambda_3+lambda_4right) d T^2$-Lipschitz - 所以原式为 $\left\{\lambda_0\left(\mu_1+\mu_2\right) D_1+\lambda_1 D_2^2+2\left(\lambda_2+\lambda_3+\lambda_4\right) d T\right\} T$-Lipschitz
- 令 $x_m$ 为vanilla Frank–Wolfe迭代m轮的结果
$$ \begin{aligned} &\min _{1 \leq j \leq m,s \geq 0,\|s\|_1 \leq \text { radius }}\left\langle\nabla f\left(x_m\right), x_m-s\right\rangle \leq \frac{\max \left\{2 h_0, 4\left\{\lambda_0\left(\mu_1+\mu_2\right) D_1+\lambda_1 D_2^2+2\left(\lambda_2+\lambda_3+\lambda_4\right) d T\right\} T\right\}}{\sqrt{m+1}} \end{aligned} $$
- 其中 $h_0=f\left(x_0\right)-\min _{x \geq 0,\|x\|_1<\text { radius }} f(x)$,$D_1$ 为 $\{|\mathcal{L}(w_i)|\}_{i\in[T]}$ 的上界,$D_2$ 为网络参数L2-norm的上界
- 在实验中 $D_2 \le 20$
- 如果 $f$ 可微且收敛,则
$$ \begin{aligned} &\min _{1 \leq j \leq m, s \geq 0,\|s\|_1 \leq \text { radius }}\left\langle\nabla f\left(x_m\right), x_m-s\right\rangle \leq \frac{8\left\{\lambda_0\left(\mu_1+\mu_2\right) D_1+\lambda_1 D_2^2+2\left(\lambda_2+\lambda_3+\lambda_4\right) d T\right\} T}{m+1} \end{aligned} $$
- 所以$\min _{b_t^o \geq 0,\left\|b_t^o\right\|_1 \leq radius} f\left(b_t^o\right)$ 的收敛率介于 $\frac{1}{m}$ 和 $\frac{1}{\sqrt{m}}$ 之间
实验验证
实验环境
Gym-minigrid:局部可观测的网格类环境,agent需要找到钥匙打开门
- 通过设置不同的障碍物和不同的要求,生成任务
DistShift、Doorkey、DynamicObstacles等 - 每个环境都可以通过调节大小和复杂性生成不同难度的任务,并构成课程学习
- 随机选择9个环境,每个环境包含至少3个难度的任务
- https://github.com/maximecb/gym-minigrid
- 通过设置不同的障碍物和不同的要求,生成任务
Meta-world:
- 50个与模拟机械臂操纵相关的任务
- MT1、MT10和MT50分别具有1、10和50个任务
- https://github.com/RchalYang/metaworld
Atari:
Arcade Learning Environment (ALE) 是Atari 2600 games的一个实验框架
- ==原文作者好像写错了名字,不是Atari,而是Arcade,虽然本质上是Atari游戏==
- Atari游戏包含了探索、规划、快速反应和复杂的视觉输入
- 随机选择的十个环境为:
YarsRevenge,Jamesbond,FishingDerby,Venture,DoubleDunk,Kangaroo,IceHockey,ChopperCommand,Krull和Robotank - https://github.com/mgbellemare/Arcade-Learning-Environment
Ravens:
- 基于PyBullet实现的基于视觉的机器人操纵环境
- 选择十个典型的离散时间桌面操纵任务:
lock-insertion,Place-red-in-green,Towers-of-hanoi,Align-box-corner,Stack-block-pyramid,Palletizing-boxes,Assembling-kits,Packing-boxes,Manipulating-rope和Sweeping-piles - 通过Ravens提供的oracle为每项任务生成1000个专家示范进行模仿学习。之后再进行10000 epoch的无示范训练,比较平均成功率
- https://github.com/google-research/ravens
RLBench:
- 为加快视觉引导下的操纵研究设计的大规模环境
- 十个典型RLBench任务:
Reach Target,Push Button,Pick And Lift,Pick Up Cup,Put Knife on Chopping Board,Take Money Out Safe,PutMoneyInSafe,PickUpUmbrella,StackWine和Slide Block To Target. - https://github.com/stepjam/RLBench
Baseline:
- AC:Single AC
- SAC:Single SAC
MRCL:Mastering rate based curriculum learning
YOLOR:You only learn one representation: Unified network for multiple tasks
Distral:Robust multitask reinforcement learning
- PCGrad:Gradient Surgery
- SM:Soft Modularization
评估指标
- Reward指标:Gym-minigrid、Meta-World、Atari
- success rate指标:Ravens、RLBench
实验结果
- Results on gym-minigrid
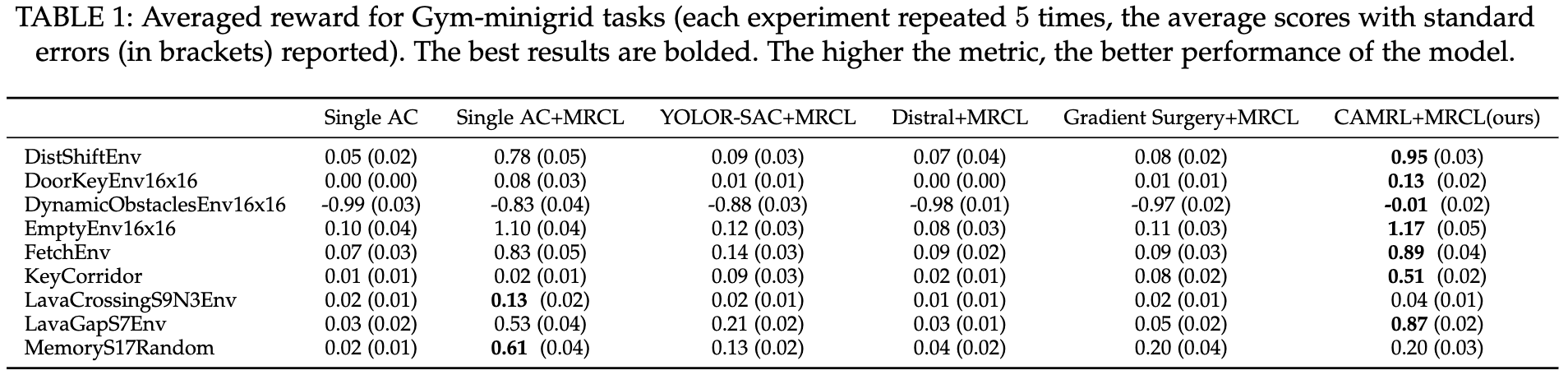
- Results on MT10 and MT50
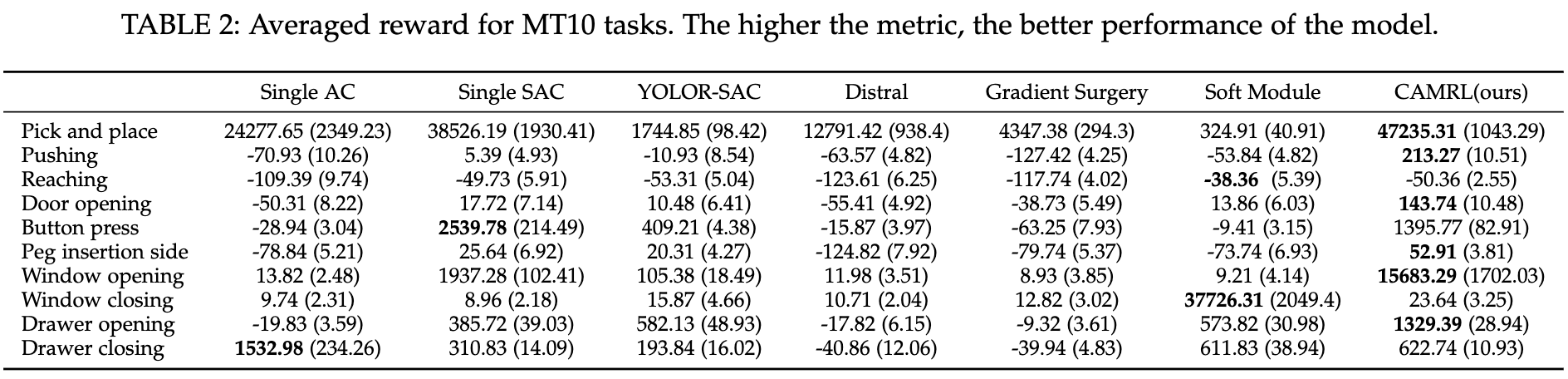
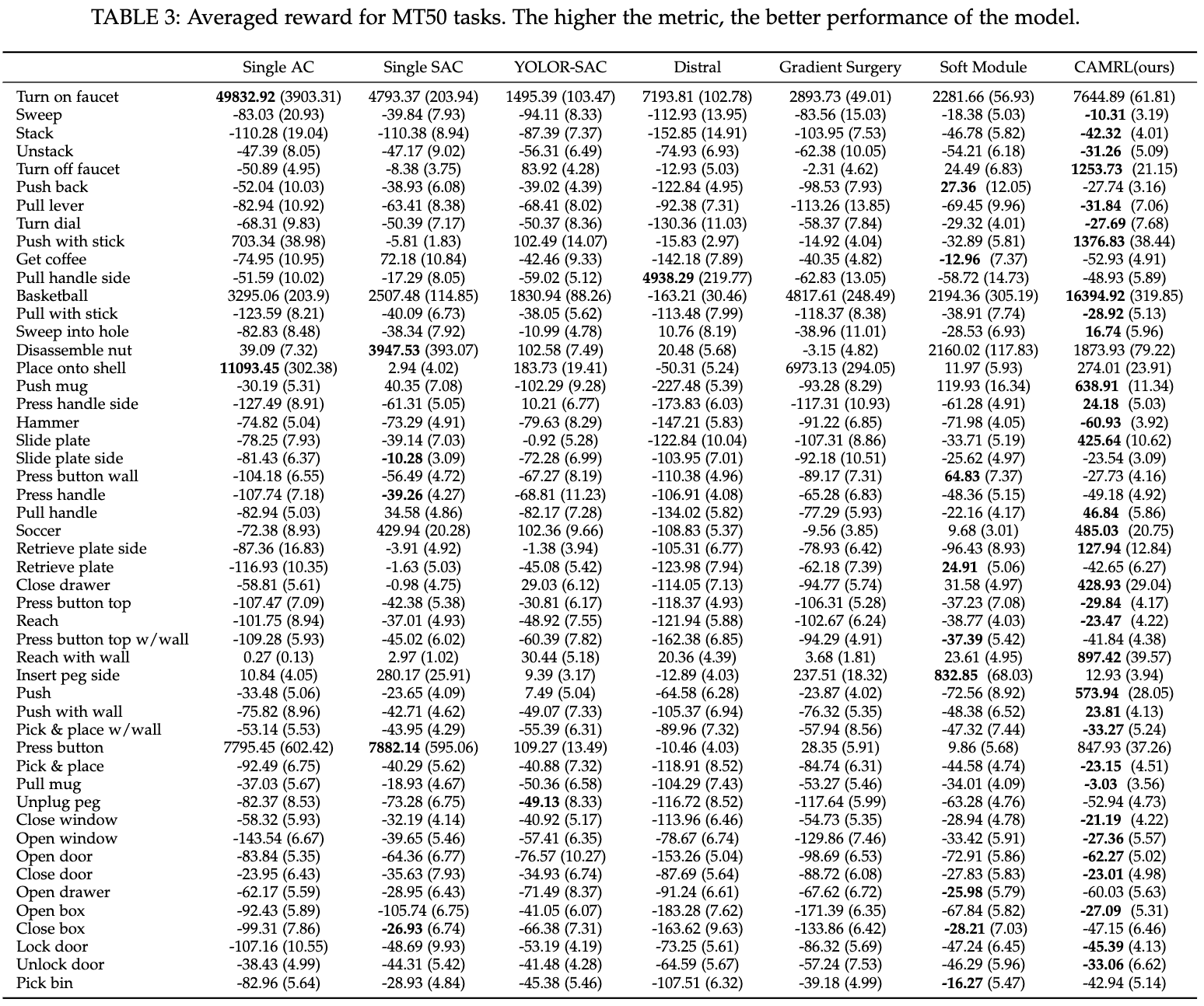
- Results on Atari
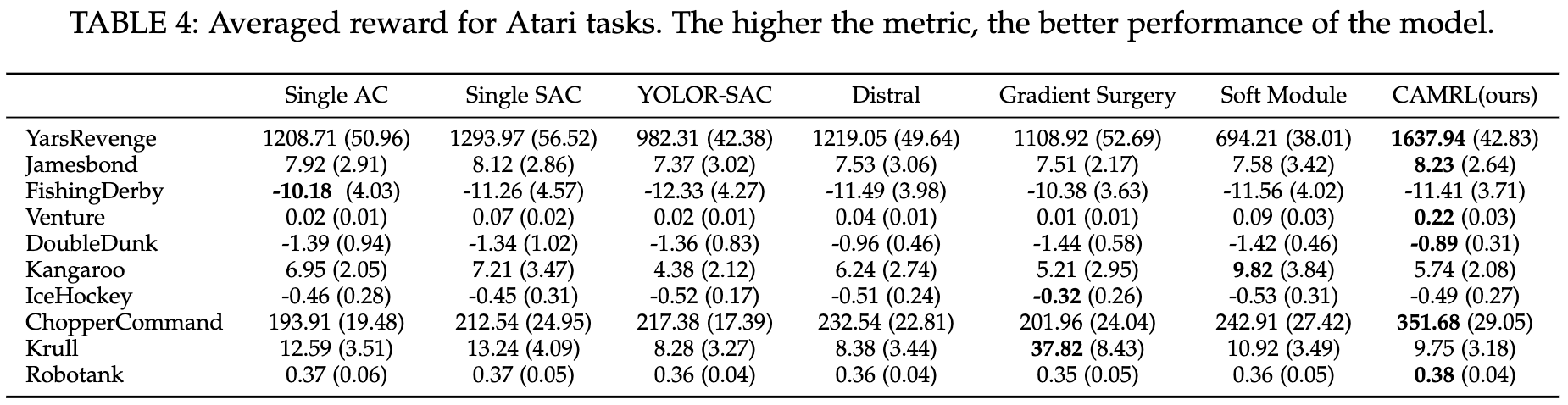
- Results on Ravens
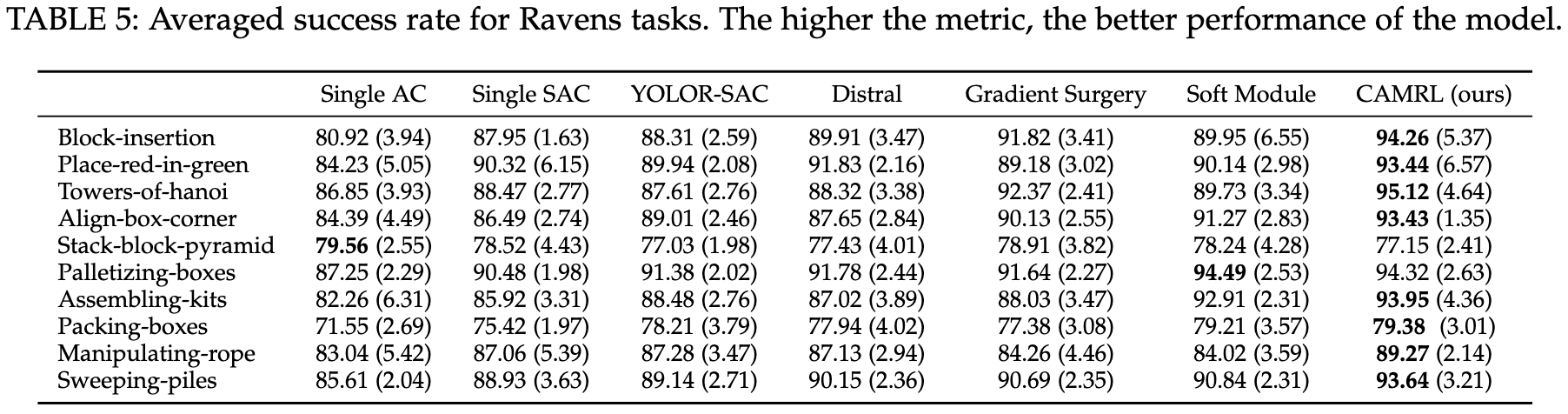
- Results on RLBench
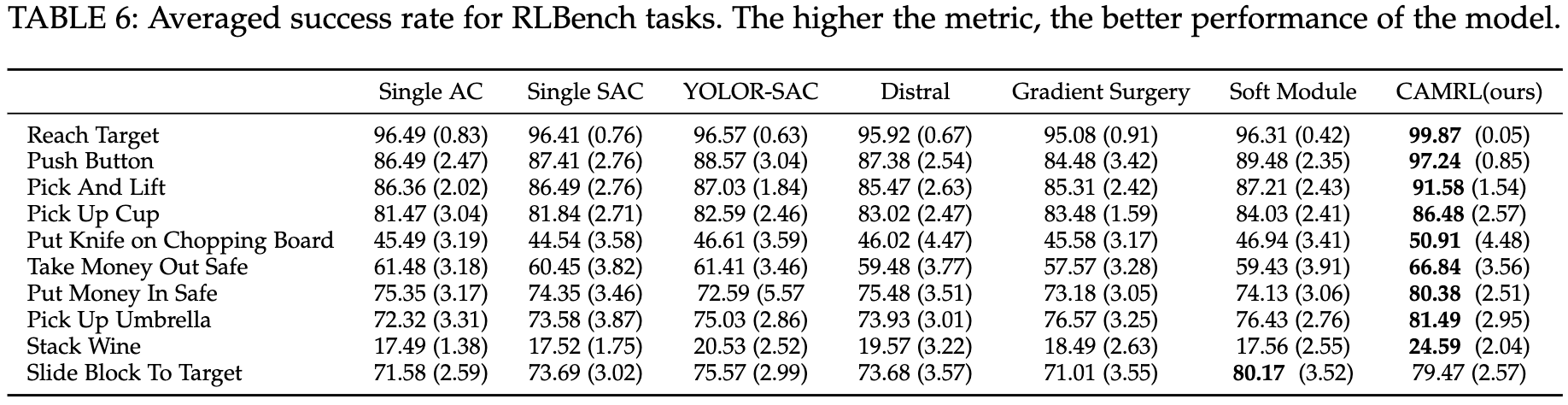
Analysis on the transfer matrix $B$
- $PR$:[Expectation 1] 对应的迁移性能排名;即 $PR_{s,t}$ 表示在任务 $s$ 上训练10k episode后在任务 $t$ 上的测试reward
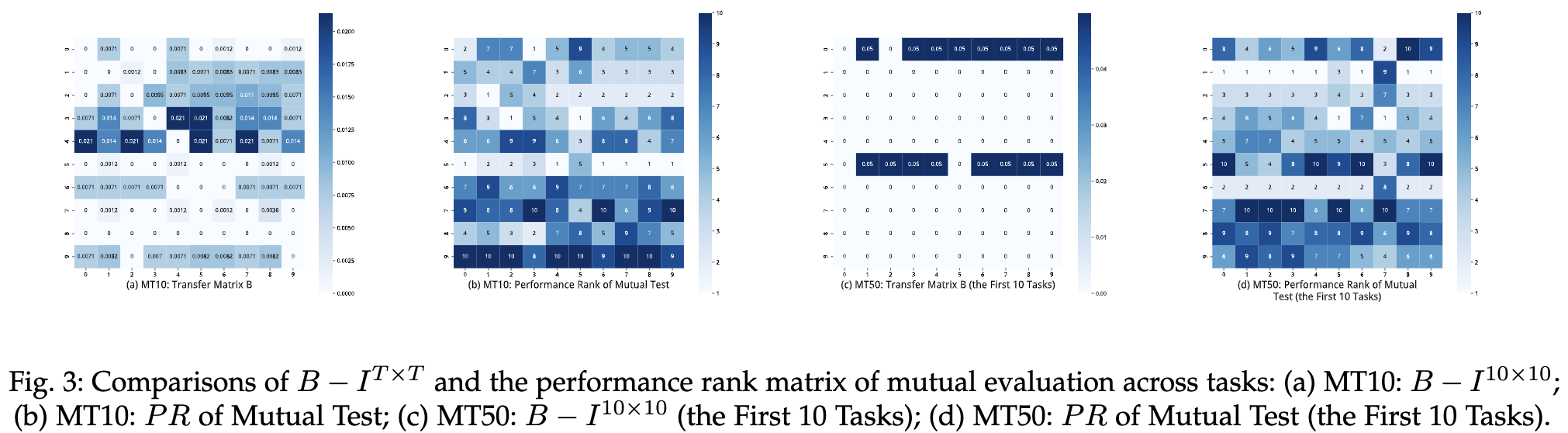
Incorporation of prior knowledge
- 使用现有state-of-the-arts方法判断任务的公开表现:任务越简单,则任务表现越好,任务收到的迁移越少
- 使用该相对排名替换掉tanh-based的可微ranking loss
- 实验结果显示在某些任务上表现更好,详细实验结果在文章附录,内容较多此处不展示了
Changes of each term in $I_{mul}$
- 可视化训练过程 $I_{mul}$ 中三项的动态变化过程
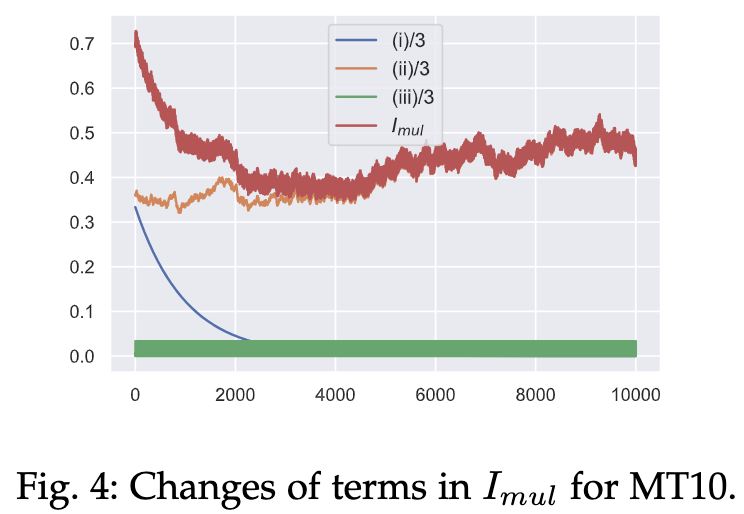
Hyper-parameter analysis
$\lambda_0=1, \mu_1=\mu_2=\lambda_1=\lambda_2=\lambda_3=\lambda_4=0.01,a=1000,b=\frac{1}{40},c=2,d=200,radius=0.05$
因为本文超参数太多了这里再说明一下各个超参数的来源
- $\lambda_0, \mu_i(i\in[2]),\lambda_j(j\in[4])$ 为损失函数对应的超参数
- $a,b,c$ 为计算 $I_{mul}$ 对应的三个超参数(用于判断下一个epoch的训练方式)
- $d$ 为构建的tanh可微分排名函数对应的超参数
- $radius$ 为人为对迁移矩阵稀疏度的限制条件 $\|b_t^o\|_1 \le radius$
实验表明上述参数为最佳,实验方法均为固定其他的修改单一超参数,详细图示见原文附录
- ==但原文附录Fig.8好像少了一幅图==
Ablation study
- 对添加的一些模块做消融实验,直接通过超参数配置即可完成
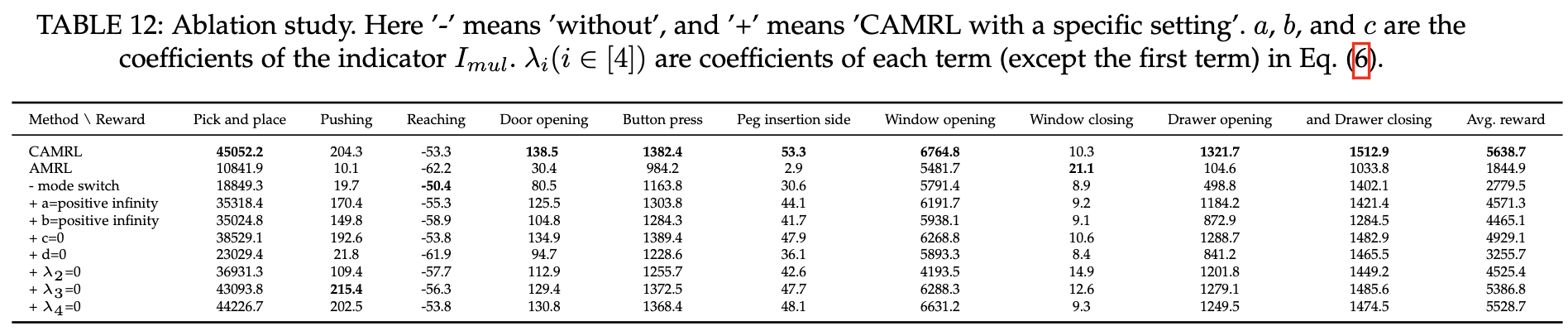
其他思考
很庆幸同时读了两篇比较类似的文章PaCo在之前有分享过,这里简单对比一下两个算法
两个算法的核心部分很类似,用于每个任务的SAC网络参数可以看作是一个参数组合
- PaCo:$\theta_{\tau} = \Phi \mathbf{w}_\tau$;CAMRL:$w_t \approx \sum_{s=1}^TB_{st}w_s$
但两个算法对于这个参数组合的解释,或者motivation不太一样
- PaCo:参数共享角度,将参数区分为共享参数 $\Phi$ 和独立参数 $w_\tau$
- CAMRL:参数被区分为任务基础参数 $w_s$ 和实际参数 $w_t$,实际参数看作是基础参数的迁移
- 由于两个算法的motivation不一样,所以对应的训练方式和损失函数就完全不同
最后简单谈一下对fast-adaption的区别(这里fast-adaption不一定准确,主要针对新的任务如何适应)
- PaCo:共享参数不变,学习独立参数,如果独立参数不足以满足,则新增共享参数
- CAMRL:会新建一个该任务的基础参数,新的任务通过课程学习学习迁移权重
- 本文在很多MTRL的Benchmark上进行了实验,实验量是非常大的,也对该领域的常用环境进行了一个汇总。可惜代码并没有提供一套统一的框架去对接不同的环境,只是简单的提供了不同算法的单一py文件。
- 本文不确定是不是有很多先前工作进行的融合,但好像没了解到类似工作的发表。毕竟第一次遇到12个超参数的网络,这个数量有点过于庞大了,个人感觉不太友好。而且可以看到每一个辅助loss其实设计都非常简单,都是一个L2 loss,就我个人而言这种rank排序对齐的方法说服力不强。而且本文提出的自动调参方法比较局限。
- 最后简单吐槽一下,发表在TPAMI这种顶刊上的文章感觉还是有不少的错误表述,甚至有少图的情况,emmm不过多评论
