ICLR2022 Workshop

摘要

Multi-task reinforcement learning (RL) algorithms can train agents to acquire generalized skills across various tasks. However, jointly learning with multiple tasks can induce negative transfer between different tasks, resulting in unstable training. In this paper, we newly propose a task representation method that prevents negative transfer in policy learning. The proposed method for multi-task RL adopts a task embedding network in addition to a policy network, where the policy network takes the output of the task embedding network and states as inputs. Furthermore, we propose a measure of negative transfer and design an overall update method that can minimize the suggested measure. In addition, we raise an issue of the negative effect on soft Q-function learning resulting in unstable Q learning and introduce the clipping method to reduce this issue. The proposed multi-task algorithm is evaluated on various robotics manipulation tasks. Numerical results show that the proposed multi-task RL algorithm effectively minimizes negative transfer and achieves better performance than previous state-of-the-art multi-task RL algorithms.

多任务强化学习（RL）算法可以训练智能体获得跨越各种任务的通用技能。然而，多任务联合学习会诱发不同任务之间的负迁移，从而导致不稳定的训练。在本文中，我们新提出了一种任务表示方法，以防止策略学习中的负迁移。所提出的多任务RL方法在策略网络之外还采用了任务嵌入网络，其中策略网络将任务嵌入网络的输出和状态作为输入。此外，我们提出了一个负转移的衡量标准，并设计了一个整体的更新方法，可以使建议的衡量标准最小化。此外，我们提出了对Soft Q函数学习的负面影响导致不稳定的Q学习的问题，并引入了剪裁方法来缓解这一问题。所提出的多任务RL算法在各种机器人操纵任务上进行了评估。数值结果表明，所提出的多任务RL算法有效地减少了负迁移，并取得了比以前最先进的多任务RL算法更好的性能。

研究动机

• 智能体用多个任务训练一个神经网络，通过在不同的任务中共享和重复使用参数来提高采样效率。

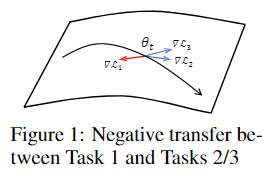
• negative transfer导致多任务学习不稳定，可以直接从策略和Q函数上进行优化。

  • 其他解决方案：对梯度进行裁剪操作；将策略划分为多个模块

主要贡献

• 提出一种任务表示方法，有效地限制了策略学习中的negative transfer
• 根据每个任务的策略更新来衡量negative transfer量，并通过基于梯度的元学习方法来训练任务嵌入网络以最小化该值
• 分析不同任务之间Q值的干扰，并在Q值上引入一种简单的裁剪方法，从而稳定Q学习

方法描述

假设每个任务有独立的soft Q函数$Q_i^\pi(s,a)$，使用SAC损失训练$J^{Q}(\psi)=\mathbb{E}_{s \sim \rho, a \sim \pi}\left[\frac{1}{2}\left(Q_{\psi}(s, a)-\left(r(s, a)+\gamma \mathbb{E}_{s^{\prime}, a^{\prime}}\left[Q_{\bar{\psi}}\left(s^{\prime}, a^{\prime}\right)-\beta \log \pi_{\theta}\left(a^{\prime} \mid s^{\prime}\right)\right]\right)\right)^{2}\right]$，每个任务有个熵系数$\beta_i$，通过$J\left(\beta_{i}\right)=\mathbb{E}_{a \sim \pi, \mathcal{T}_{i}}\left[-\beta_{i} \log \pi(a \mid s, z)-\beta_{i} \bar{H}\right]$优化。

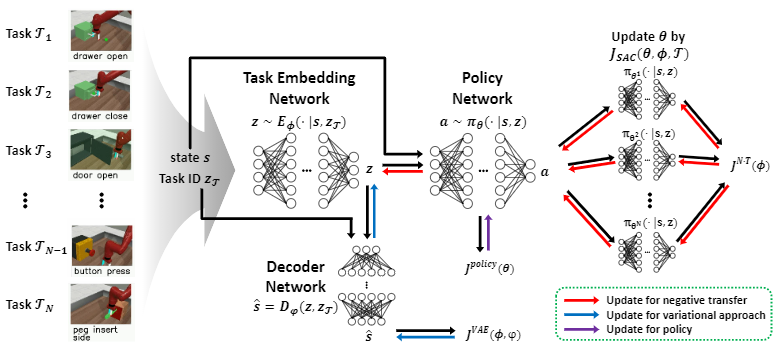
• 带任务嵌入网络的策略网络

  • 策略网络：$\pi_\theta(a|s,z)$，其中$z$为任务嵌入网络的输出，即任务表征
  • 任务嵌入网络：$E_\phi(z|s,z_\mathcal{T})$，其中$s_\mathcal{T}$为任务的one-hot编码

• negative transfer度量

  • 多任务目标：最大化$\mathbb{E}_{\mathcal{T} \sim p(\mathcal{T})}[J_{SAC}(\theta, \phi, \mathcal{T})]$，其中$\theta$为策略网络参数，$\phi$为任务嵌入网络参数
  • 定义目标集和：$J_{set} = \{J_{SAC}(\theta,\phi,\mathcal{T}_j) \}_{j=1}^N$
  • 单个任务对策略网络的更新参数：$\theta^i=\theta + \alpha \nabla_\theta J_{SAC}(\theta,\phi, \mathcal{T}_i)$，其中$\alpha$表示更新步长
  • 新目标集和：$J_{set}^i = \{J_{SAC}(\theta^i,\phi,\mathcal{T}_j) \}_{j=1}^N$
  • 任务$i$更新导致的Negative Transfer：$\mu(\mathcal{T}_i) = |\{j|J_{SAC}(\theta^i, \phi, \mathcal{T}_j) < J_{SAC}(\theta, \phi, \mathcal{T}_j)\}|$，即导致其他任务性能下降的任务数量

• 策略网络训练

  • 任务选择：选取Negative Transfer影响最小的$M$个任务，即$C_s:=\{\mathcal{T}_j|\mu(\mathcal{T}_j) \le \mu(\mathcal{T}_{\kappa(M)}) \}$，其中$\kappa(i) = \arg\min_{k\in\{1,\dots,N\}, k\notin\{\kappa(1),\dots,\kappa(i-1)\}} \mu(\mathcal{T}_k)$

  • $C_s$中不同任务的更新权重：$w_i = \frac{\exp(N-\mu(\mathcal{T}_i))}{\sum_{j=1}^M \exp(N-\mu(\mathcal{T}_j))}$

    • ==个人人为原文表达有误，此为个人认为的可能解释，原文中将此处$M$替换为$N$==

  • 整体策略目标函数：$J^{policy}(\theta)=\sum_{i=1}^M w_i J_{SAC}(\theta, \phi, \mathcal{T}_i)$

    • ==原文此处的$M$仍为$N$==

• 任务嵌入网络训练

  • $E_\phi$的目标是减少所有任务的$\mu(\mathcal{T}_k)$
  • 对任意$\mathcal{T}_k$最大化平均新目标集和：$J^{N\cdot T}(\phi, \mathcal{T}_k) = \frac{1}{N}\sum_{i=1}^N[J_{SAC}(\theta^k, \phi, \mathcal{T}_i)] = \frac{1}{N}\sum_{i=1}^N[J_{SAC}(\theta + \alpha\nabla_\theta J_{SAC}(\theta,\phi,\mathcal{T}_k), \phi, \mathcal{T}_i)]$，该优化目标表示针对$\pi_{\theta^k}$的优化，而非$\pi_\theta$，类似基于梯度的元学习方法
  • 仅针对有害任务进行训练，即$\mathcal{T} \in C \setminus C_s$
  • negative transfer任务嵌入最终目标函数：$\widehat{J}^{N \cdot T}(\phi) = \frac{1}{C \setminus C_s} \sum_{\mathcal{T} \in C \setminus C_s} J^{N \cdot T}(\phi, \mathcal{T})$
  • 变分表征学习：构建解码网络$D_\varphi(z,z_\mathcal{T})$还原状态信息
  • 变分额外目标：$J^{VAE}(\phi,\varphi)=\mathbb{E}_{\mathcal{T} \sim p(\mathcal{T})} \left[ \mathbb{E}_{z \in E_\phi, s \in \mathcal{T}} \left[ |D_\varphi(z,z_{\mathcal{T}}) - s|^2 + D_{KL}(E_\phi(\cdot|s,z_\mathcal{T}), p(z)) \right] \right]$，其中$p(z)$为标准正态分布

• Soft Q函数的负面影响

  • 每个任务独立更新Soft Q函数：$J^{Q}\left(d, \psi^{i}\right)=\frac{1}{2}\left(Q_{\psi^{i}}(s, a)-\left(r+\gamma \mathbb{E}_{a^{\prime} \sim \pi, z \sim E_{\phi}}\left[Q_{\bar{\psi}^{i}}\left(s^{\prime}, a^{\prime}\right)-\beta \log \pi_{\theta}\left(a^{\prime} \mid s^{\prime}, z\right)\right]\right)\right)^{2}$
  • 如果当前策略$\theta$受其他任务影响较大，则target网络对$Q(s',a')$的估计误差较大，因为当前策略的分布与采样分布差别较大
  • Q Loss裁剪：$J_{CLIP}^Q(\psi^i) = \mathbb{E}_{d=(s,a,r,s') \sim D} \left[ \text{clip}(J^Q(d,\psi^i), 0, V_{\text{clip}}) \right]$，其中$D$是一个mini-batch，$V_{\text{clip}}$是不需要clip的最大值

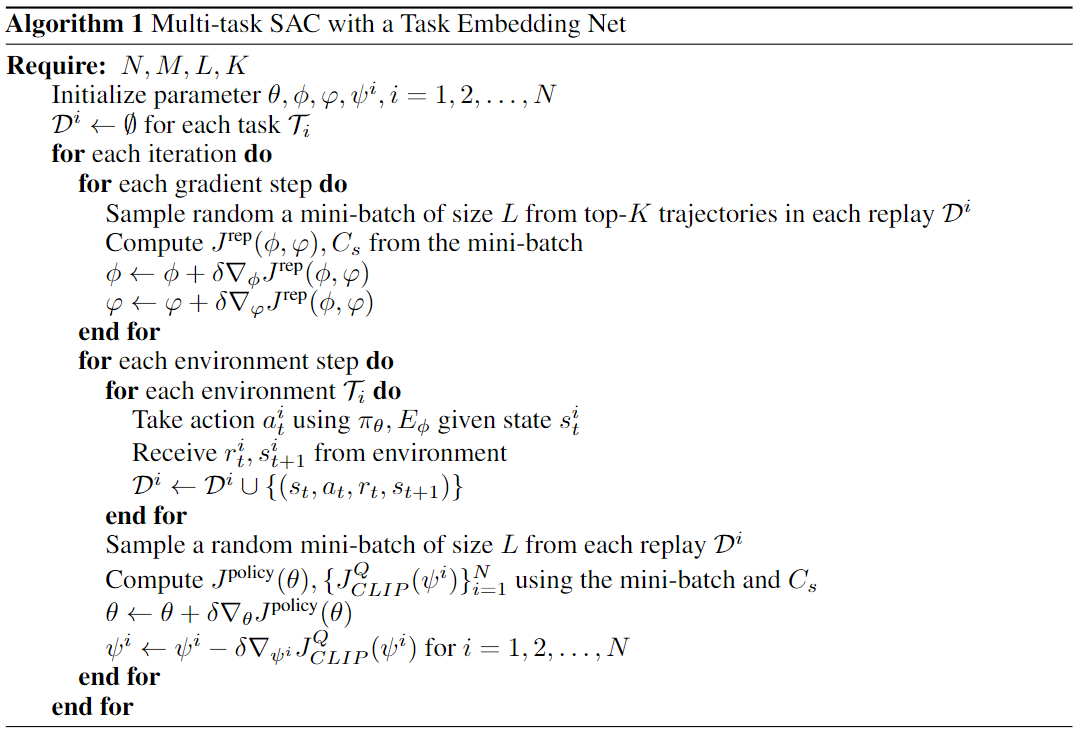
• Top-K经验回复

  • 每$H$步重新选择任务集合$C_s$，其中$H$是环境长度
  • 为减少任务选择的不确定性，每个任务构建一个新的经验回放池存储Top-K个回报最高的trajectory，使用该回放池训练任务嵌入网络$E_\phi$

理论分析

无

实验验证

• 实验环境

  • 不同任务的奖励函数和转移函数不同，共享状态空间和动作空间
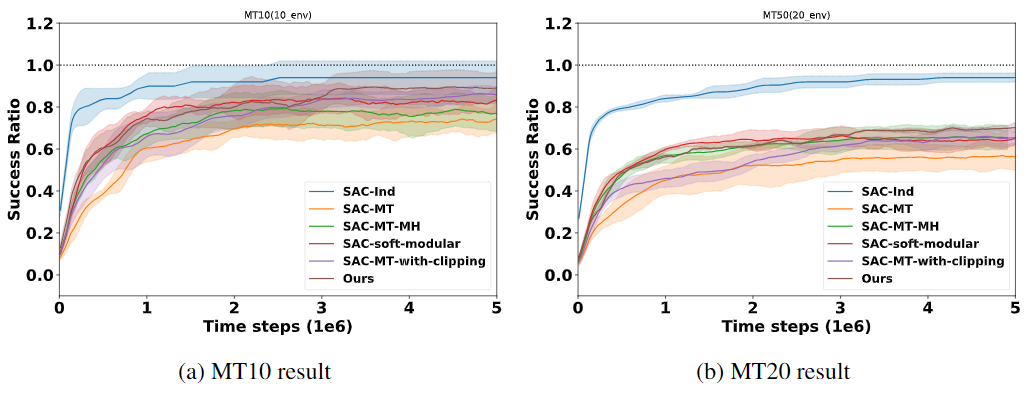
  • Meta-World：MT10 & MT20

• Baselines

  • SAC-Ind：独立任务SAC
  • SAC-MT：状态+任务one-hot作为输入
  • SAC-MT-MH：Policy最后一层网络为multi-head
  • SAC-soft-modular：软模块化路由网络 http://darkdawn.top/index.php/archives/22/
  • SAC-MT-with-clipping：SAC-MT with soft Q-function裁剪
• 整体实验结果

• 消融实验

  • Effects on Method for Preventing Negative Transfer

    • train frequency：在20个episode内被训练的概率，可以间接反映$\mu(\mathcal{T}_k)$的大小，$\mu(\mathcal{T}_k)$越小则训练频率越高
    • 当任务在训练初期快速学习时会导致Negative Transfer快速增大（训练频率下降），但该方法在训练频率较低的情况下仍保持高胜率

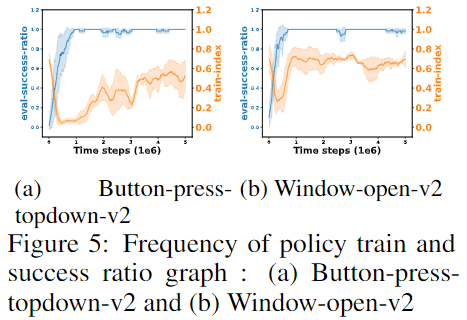
• Effects on Clipping Method

  • SAC-MT-with-clipping可以在SAC-MT基础上有效提高任务的性能

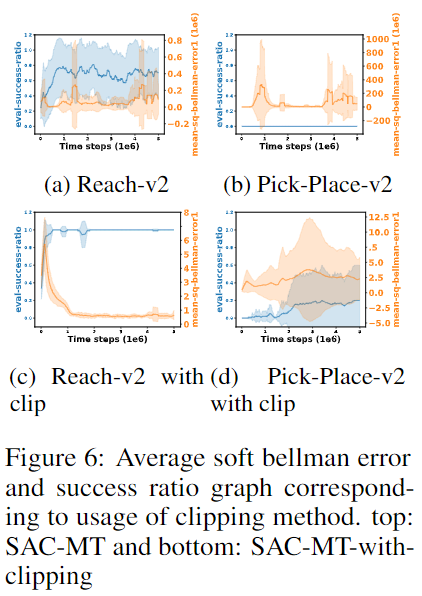
• Effect of Components of Our Method

  • VAE是对性能影响最大的部分：说明学到好的任务表征很重要

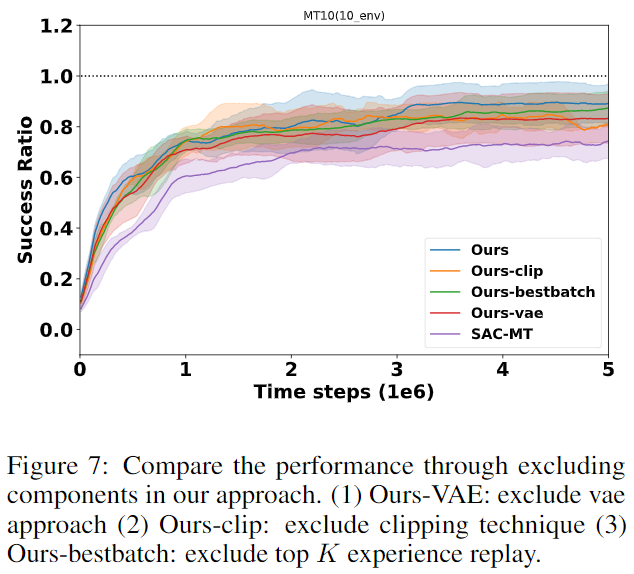
其他思考

• 个人认为该方法中最新颖的部分应该是利用表征学习来缓解梯度冲突，若梯度冲突小则学习策略，若梯度冲突大利用任务表征网络尽量减少学习策略的梯度冲突
• 关于任务选择部分好像存在一些问题（例如一共5个任务，任务1，2分别和任务3，4，5不冲突，但其他任意两个任务两两冲突，满足$\mu(\mathcal{T}_1)=\mu(\mathcal{T}_2)=3>\mu(\mathcal{T}_3)=\mu(\mathcal{T}_4)=\mu(\mathcal{T}_5)=2$，此时会选择任务1和2进行策略更新，但此时二者本身构成冲突），此为一个直观举例，并无详细理论说明，可能存在错误。如果存在该问题，是否可以通过构建任务冲突关系图来解决，最直观的方法就是寻找互不冲突的任务最大团。
• 作者的motivation是为了缓解negative transfer（可以理解为梯度冲突造成的负影响），可惜没有直接和梯度操作的方法进行对比，例如GradNorm、PCGrad等。二者对于negative transfer的理解也有所不同，直接对梯度操作的方法更细粒度（即针对网络中的具体参数进行调整）；而本文是宏观上进行定义（即最终结果，更新后的策略会使其他任务表现变差）

原文链接：https://openreview.net/forum?id=rV2zaEpNybc