ICML 2015

摘要

Value functions are a core component of reinforcement learning systems. The main idea is to to construct a single function approximator $V(s;\theta)$ that estimates the long-term reward from any state $s$, using parameters $\theta$. In this paper we introduce universal value function approximators (UVFAs) $V (s,g;\theta)$ that generalise not just over states $s$ but also over goals $g$. We develop an efficient technique for supervised learning of UVFAs, by factoring observed values into separate embedding vectors for state and goal, and then learning a mapping from $s$ and $g$ to these factored embedding vectors. We show how this technique may be incorporated into a reinforcement learning algorithm that updates the UVFA solely from observed rewards. Finally, we demonstrate that a UVFA can successfully generalise to previously unseen goals.

价值函数是强化学习系统的一个核心组成部分。其主要思想是构建一个单一的函数近似器$V(s;\theta)$，使用参数$\theta$估计任何状态$s$的长期奖励。在本文中，我们引入了通用价值函数近似器（UVFAs）$V (s,g;\theta)$，它不仅适用于状态$s$，也适用于目标$g$。我们为UVFAs的监督学习开发了一种有效的技术，通过将观察到的值分解成独立的状态和目标的嵌入向量，然后学习从$s$和$g$到这些分解的嵌入向量的映射。我们展示了这一技术如何被应用于强化学习算法，该算法仅从观察到的奖励中更新UVFA。最后，我们证明UVFA可以成功地推广到以前未见过的目标。

研究动机

状态价值函数逼近器$V(s; \theta)$利用状态空间的结构，有效地学习观察到的状态的值，并归纳出类似的、未见过的状态的值。目标空间通常和状态空间一样包含大量结构信息，所以目标空间也可以用类似的方法进行归纳和推测。

主要贡献

  • 提出通用函数逼近器UVFA $V(s,g;\theta)$
  • 利用低秩分解将价值$V_g(s)$分解为状态嵌入$\phi(s)$和目标嵌入$\psi(g)$
  • 强化学习中，利用bootstrapping更新的方法端到端地训练UVFA

方法描述

广义值函数：$V_{g, \pi}(s):=\mathbb{E}\left[\sum_{t=0}^{\infty} R_{g}\left(s_{t+1}, a_{t}, s_{t}\right) \prod_{k=0}^{t} \gamma_{g}\left(s_{k}\right) \mid s_{0}=s\right]$

广义动作价值函数：$Q_{g, \pi}(s, a):=\mathbb{E}_{s^{\prime}}\left[R_{g}\left(s, a, s^{\prime}\right)+\gamma_{g}\left(s^{\prime}\right) \cdot V_{g, \pi}\left(s^{\prime}\right)\right]$

最优策略：$\pi_g^*(s) := \arg\max_aQ_{\pi,g}(s,a)$；最优价值函数：$V_{g}^{*}:=V_{g, \pi_{g}^{*}}$；$Q_{g}^{*}:=Q_{g, \pi_{g}^{*}}$

函数逼近器结构

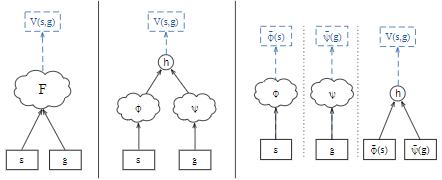
  • 通用函数逼近器两种结构：

    • Concatenated 结构（左图）：将状态$s$和目标$g$联合作为函数逼近器输入$F:\mathcal{S} \times \mathcal{G} \mapsto \mathbb{R}$（$F$表示为MLP）

    • two-stream 结构（中图右图）：

      • 因子结构子模块嵌入：$\phi:\mathcal{S} \mapsto \mathbb{R}^n$和$\psi:\mathcal{G} \mapsto \mathbb{R}^n$，再进行映射$h:\mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}$（$\phi$和$\psi$表示为MLP；$h$表示为点乘）
      • 部分对称：利用状态和目标结构上的相似性（例如$\mathcal{G} \subseteq \mathcal{S}$），可以共享网络的第一层参数
      • 完全对称：UVFA可能是对称的（例如$V_g^*(s)=V_s^*(g) \forall s,g$），可以利用相同网络

  • 监督学习两种实现：（将值函数真实值$V_g^*(s)$作为标签进行训练）

    • end-to-end端到端训练：需要合适的损失函数例如均方误差MSE $\mathbb{E}\left[ (V_g^*(s) - V(s,g;\theta))^2 \right]$

    • two-stage两阶段训练：

      • Stage 1：将所有$V_g^*(s)$置于矩阵中，行表示状态$s$，列表示目标$g$，对矩阵进行低秩分解为n维的嵌入空间，用$\hat \phi_s$表示状态target嵌入向量，$\hat \psi_g$表示目标target嵌入向量
      • Stage 2：$\phi$拟合$\hat \phi_s$；$\psi$拟合$\hat \psi_g$
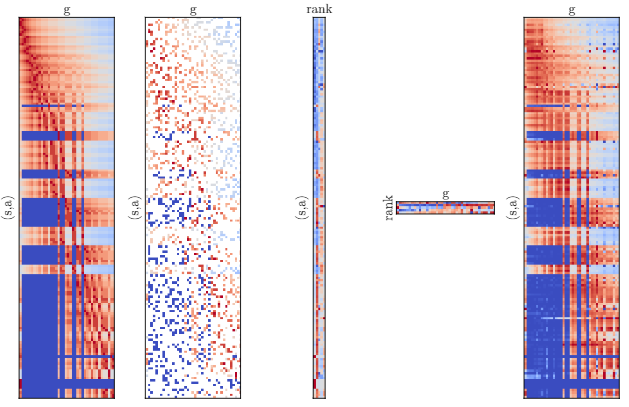
      • 下图示意低秩分解，从左至右分别是：真实Value，采样Value，分解后行向量，分解后列向量，点乘重组Value。所以$\phi$和$\psi$只需拟合5维target嵌入向量。

    2-room LavaWorld低秩分解示意

  • 强化学习两种实现：（真实$V_g^*(s)$无法获取）

    • 基于Horde的UVFA：每个demon估计一个特定目标的值函数

Horde UVFA

  • 基于bootstrapping的UVFA

    • 直接端到端更新：$ Q\left(s_{t}, a_{t}, g\right) \leftarrow \alpha\left(r_{g}+\gamma_{g} \max _{a^{\prime}} Q\left(s_{t+1}, a^{\prime}, g\right)\right) +(1-\alpha) Q\left(s_{t}, a_{t}, g\right) $
    • 同时进行bootstrapping拟合函数以及泛化目标会使学习过程变得十分不稳定()

理论分析

无

实验验证

  • 监督学习

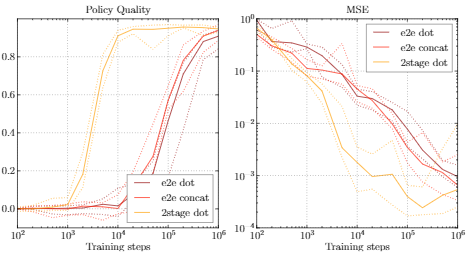
    • 结构对比（2-room 7x7 LavaWorld）

结构对比

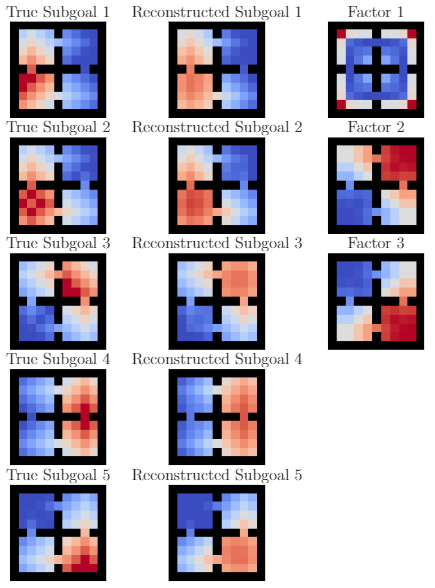
  • 低秩分解可视化（4-rooms）

低秩分解可视化

  • 低秩rank消融

低秩rank消融

  • 数据稀疏度消融

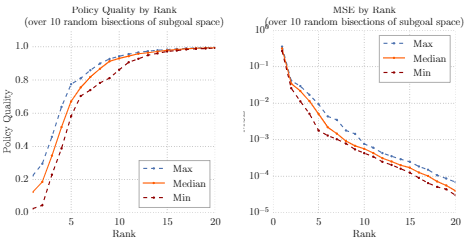
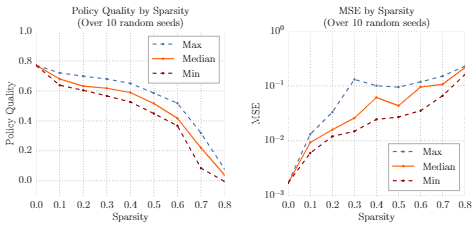
数据稀疏度消融

  • 泛化性（只在前三个房间的目标中进行训练）

泛化性

  • 强化学习

    • 直接bootstrapping的状态-目标稀疏度

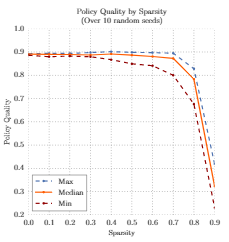
直接bootstrapping的状态-目标稀疏度

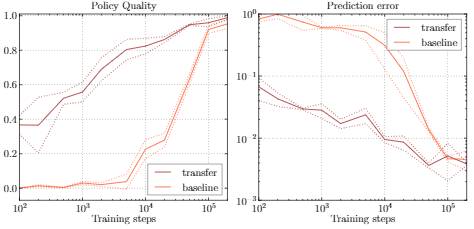
  • 迁移学习（对比从零学习）

迁移学习

其他思考

  • 本文提出了新的广义价值函数，引入了人目标的概念，单仅将目标进行了简单的形式化定义，并没有具体说明目标如何获取，文章只针对最简单的情形（目标是状态的子空间，通常表示为某一个位置）。
  • 该方法应用的难点还是在于目标的定义，在实际应用中目标可能需要更抽象的表示，例如自然语言输入。
  • two-stage的训练方法在大环境中很难适用，如何应用于大规模训练还有待探讨。

原文链接：http://proceedings.mlr.press/v37/schaul15.pdf

参考资料：https://zhuanlan.zhihu.com/p/500741089

Last modification：July 26, 2022
© Allow specification reprint
如果觉得我的文章对你有用，请随意赞赏