NeurIPS2020
摘要
While deep learning and deep reinforcement learning (RL) systems have demonstrated impressive results in domains such as image classification, game playing, and robotic control, data efficiency remains a major challenge. Multi-task learning has emerged as a promising approach for sharing structure across multiple tasks to enable more efficient learning. However, the multi-task setting presents a number of optimization challenges, making it difficult to realize large efficiency gains compared to learning tasks independently. The reasons why multi-task learning is so challenging compared to single-task learning are not fully understood. In this work, we identify a set of three conditions of the multi-task optimization landscape that cause detrimental gradient interference, and develop a simple yet general approach for avoiding such interference between task gradients. We propose a form of gradient surgery that projects a task’s gradient onto the normal plane of the gradient of any other task that has a conflicting gradient. On a series of challenging multi-task supervised and multi-task RL problems, this approach leads to substantial gains in efficiency and performance. Further, it is model-agnostic and can be combined with previously-proposed multi-task architectures for enhanced performance.
虽然深度学习和深度强化学习（RL）系统在图像分类、游戏和机器人控制等领域表现出令人印象深刻的结果，但<font color=Blue>数据效率</font>仍然是一个主要挑战。多任务学习已经成为一种很有前途的方法，可以在多个任务之间共享结构，以实现更有效的学习。然而，多任务设置带来了一些优化方面的挑战，与独立学习任务相比，它很难实现巨大的效率提升。与单任务学习相比，多任务学习具有如此大的挑战性，其原因并不完全清楚。在这项工作中，我们确定了多任务优化环境中导致有害梯度干扰的三个条件，并开发了一种简单而通用的方法来避免任务梯度之间的这种干扰。我们提出了一种梯度手术的形式，将一个任务的梯度投射到具有冲突梯度的任何其他任务的梯度的法线上。在一系列具有挑战性的多任务监督和多任务RL问题上，这种方法导致了效率和性能的大幅提高。此外，它与模型无关，可以与以前提出的多任务结构相结合，以提高性能。
研究动机
解决多任务学习的传统方法是联合训练一个有着共享部分的网络，这种办法有着较高的效率。然而和独立学习任务相比，这种办法有时候的效果不佳，而且数据利用率较低。因为在联合训练的情况下，不同任务的梯度方向和梯度量级不一样，导致共享网络部分加权的梯度有可能被量级大的任务梯度主导，那么这个有着主导作用的任务有可能就会被过估计，其他任务自然就会被欠估计。
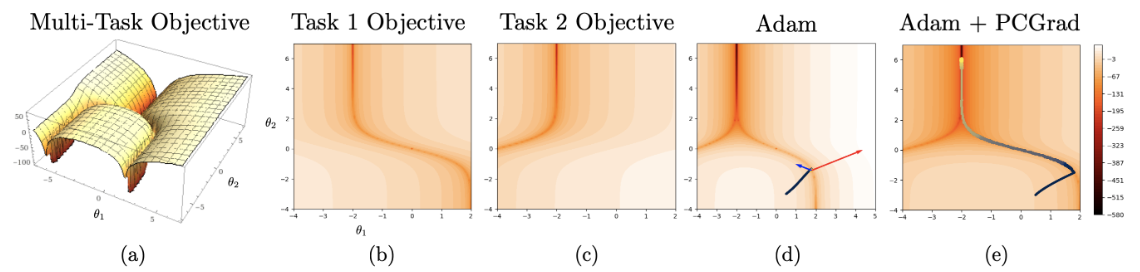
图1中即一种极端情况（极小点附近曲率非常大），(d)中黑线表示梯度下降路线，当前点距离任务1最优距离小梯度大，任务2最优距离大梯度小，导致梯度被任务1主导，任务2无法有效学习，因此收敛速度很慢。
主要贡献
- 提出一种通过直接改变梯度的方法来缓解梯度冲突——“梯度手术”；
- 该方法直接作用于梯度，与模型无关，适用性很高，适用于多任务监督学习、多任务强化学习，也可以与已有多任务学习方法结合；
- 从理论分析和实验验证上均证明该方法在数据效率、优化速度和最终性能得到较大提升。
方法描述
多任务问题描述为：$\min_\theta \mathbb{E}_{\mathcal{T}_i \sim p(\mathcal{T})} [\mathcal{L}_i(\theta)]$，其中$p(\mathcal{T})$为任务分布；
一般多任务Loss函数表示为不同任务的Loss和：$\mathcal{L}(\theta) = \sum_i \mathcal{L}_i(\theta)$；
多任务模型描述为：$f_\theta(y|x,z_i)$，其中$x$为输入，$y$为输出，$z_i$为任务$i$的one-hot编码。
本文提出的“梯度手术”方法比较简单，主要算法流程描述如下：
PCGrad: Project Conflicting Gradients
- 首先，通过计算梯度$g_i$和$g_j$之间的余弦相似度来判断是否梯度冲突；
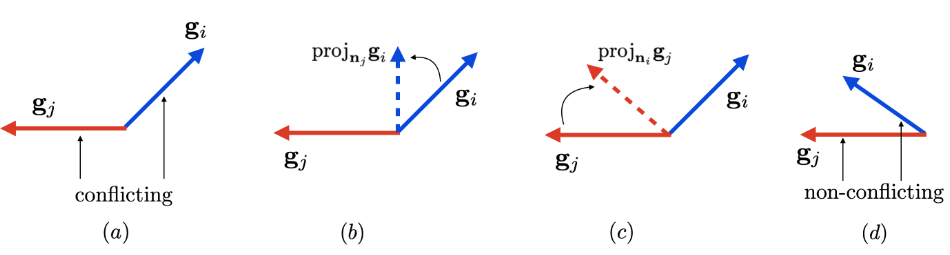
- 若梯度冲突，进行梯度手术，将$g_i$投影到$g_j$的法平面上$g_i = g_i - \frac{g_i \cdot g_j}{\|g_j\|^2}g_j$，如图2(b)所示；若梯度不冲突，则保持原梯度不变；
- 在批量数据中，以随机顺序取样所有其他任务重复此操作。对批量数据中的所有任务执行同样的操作更新梯度。
理论分析
虽然本文提供的缓解梯度冲突的方案比较简单，但其在理论方面进行了较多分析，主要针对梯度手术的收敛性和收敛速率进行了理论分析。定义1-3被作者认为是多任务优化挑战的主要因素。
- 定义1. 梯度冲突：$\cos \phi_{ij} < 0$，若两个梯度夹角大于90度即为冲突。
- 定义2. 梯度量级相似性：$\Phi(g_i, g_j) = \frac{2\|g_i\|_2\|g_j\|_2}{\|g_i\|_2^2+\|g_j\|_2^2}$，用于衡量两个梯度的大小差距。
- 定义3. 多任务曲率：$H(\mathcal{L};\theta,\theta') = \int_0^1 \nabla \mathcal{L}(\theta)^T \nabla^2 \mathcal{L}(\theta + a(\theta' - \theta)) \nabla\mathcal{L}(\theta) da$，用于表示迭代前后Loss曲率变化。
- 定义4. 两个任务的学习目标为$\mathcal{L}(\theta) = \mathcal{L}_1(\theta) + \mathcal{L}_2(\theta)$，梯度表示为$g_1 = \nabla \mathcal{L}_1(\theta), g_2 = \mathcal{L}_2(\theta), g = g_1 + g_2$
- 定理1.（证明PCGrad的收敛性）假设$\mathcal{L}_1$和$\mathcal{L}_2$是凸函数且可微，$\mathcal{L}$的梯度是Lipschitz连续的对$L > 0$成立，则PCGrad更新规则在步长$t \le \frac{1}{L}$的情况下会收敛到 (a) 位置$\cos(\phi_{12})=-1$ 或 (b) 最优点$\mathcal{L}(\theta^*)$。由于条件(a)很难达成，所以基本会收敛到最优点。
- 定义5. 多任务曲率边界：$\xi(g_1,g_2) = (1 - \cos^2\phi_{12})\frac{\|g_1-g_2\|_2^2}{\|g_1+g_2\|_2^2}$
定理2.（证明PCGrad的收敛速度）假设$\mathcal{L}$可微，且其梯度是Lipschitz连续的对$L > 0$成立。$\theta^{MT}$为原参数，$\theta^{PCGrad}$为手术后梯度。假设$H(\mathcal{L};\theta,\theta^{MT}) \ge l\|g\|_2^2$，且$l \le L$，即多任务曲率满足下界。则如果满足 (a) $cos{\phi_{12}} \le - \Phi(g_1,g_2)$；(b) $l \ge \xi(g_1,g_2)$；(c) $t \ge \frac{2}{l-\xi(g_1,g_2)L}$，则$\mathcal{L}(\theta^{PCGrad}) \le \mathcal{L}(\theta^{MT})$。
- 用文字表述定理2为：若满足 (a) 任务梯度冲突；(b) 任务量级差距大；(c) 多任务梯度曲率大；(d) 学习率足够大，则与多任务学习中的标准梯度下降相比，PCGrad的收敛速率更快。
实验验证
本文在多任务监督学习、多任务强化学习、多任务多目标强化学习环境中均进行实验，这里主要分析强化学习实验结果。
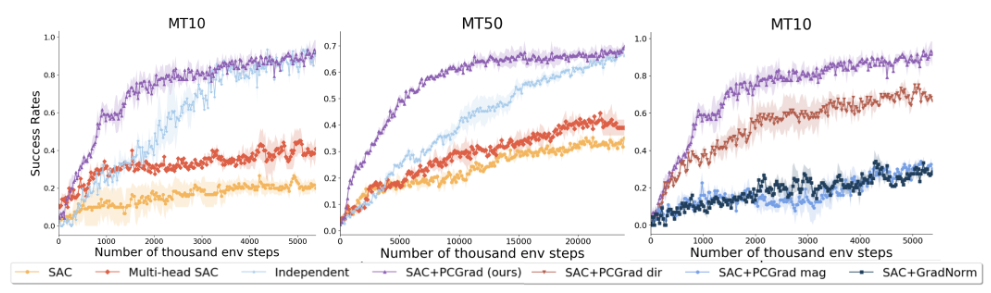
- 实验环境：Meta-World（MT10、MT50），即分别使用机械臂完成10和50个任务。
- Baselines：SAC（不进行任务区分）、Multi-head SAC（共享网络后针对不同任务有独立网络）、Inde-pendent（所有任务独立训练）
- Ablation：SAC+PCGrad dir（只对方向进行手术）、SAC+PCGrad mag（只对量级进行手术）、SAC+GradNorm（其他工作，对梯度量级进行缩放）
同时本文对理论分析中多任务优化挑战的主要因素进行了实验可视化分析如图5所示，在两个任务的环境中进行测试。
其中，左图展示了在整个训练中多任务曲率的曲率呈指数级上升，即确实面临高曲率问题；中图展示了随着训练的过程，梯度冲突的情况更加频繁出现；右图表示训练过程中的确存在梯度被一个任务主导导致另一任务无法有效学习的情况。
其他思考
- 图5中如果结合三图一起进行分析，右图显示在迭代步数45步左右时，任务2开始被有效学习，此时在左图和中图中并无明显条件表示此时学习进行了什么特殊的变化；
- 文中的理论分析均针对两个任务进行分析，此时梯度手术可以缓解冲突，但如果任务数量变多，会导致梯度手术出现冲突，例如三个任务的梯度两两冲突（在同一平面中任意两个梯度夹角为120度），此时是否还能保证收敛。文中仅用随机的任务序列解决该问题，即若冲突依次投影到后续梯度法平面。
One comment
何大哥棒棒！